4. Metrics
Authors: Valentin Christiaens and Carlos Alberto Gomez GonzalezSuitable for VIP v1.0.0 onwardsLast update: 2024/03/25
Table of contents
This tutorial shows:
how to compute the S/N ratio of a given companion candidate;
how to calculate the significance of a detection;
how to compute S/N ratio maps and STIM maps;
how to use the automatic point-source detection function;
how to compute throughput and contrast curves;
how to compute robust contrast curves and contrast grids with Applefy (requires the installation of ``Applefy`` – details here).
Disclaimer on multi-processing
A number of routines in the metrics subpackage have been implemented for compatibility with multiprocessing, in order to optimally harness the power of machines equipped with multiple CPUs. Any function where the nproc parameter is available in its call (or which internally calls a psfsub function, such as the contrast curve function) can be run in multi-processing, with the value of nproc setting the requested number of CPUs to use. Instead of an integer, one can set
nproc=None to use half of all available CPUs. For optimal results in multiprocessing, set the following environment parameters BEFORE launching your Jupyter notebook:
export MKL_NUM_THREADS=1
export NUMEXPR_NUM_THREADS=1
export OMP_NUM_THREADS=1
Let’s first import a couple of external packages needed in this tutorial:
[1]:
%matplotlib inline
from hciplot import plot_frames, plot_cubes
from matplotlib import pyplot as plt
import matplotlib.gridspec as gridspec
from multiprocessing import cpu_count
import numpy as np
import os
from packaging import version
from scipy import interpolate
# Seaborn is only necessary to plot Applefy contrast grid results.
# It is not a mandatory requirement of VIP (only one cell will not compile in this notebook).
try:
import seaborn as sns
no_sns=False
except:
no_sns=True
In the following box we check that your version of VIP passes the requirements to run this notebook:
[2]:
import vip_hci as vip
vvip = vip.__version__
print("VIP version: ", vvip)
if version.parse(vvip) <= version.parse("1.0.3"):
msg = "Please upgrade your version of VIP"
msg+= "It should be striclty above 1.0.3 to run this notebook."
raise ValueError(msg)
VIP version: 1.6.0
4.1. Loading ADI data
In the ‘dataset’ folder of the VIP_extras repository you can find a toy ADI (Angular Differential Imaging) cube and a NACO point spread function (PSF) to demonstrate the capabilities of VIP. This is an L’-band VLT/NACO dataset of beta Pictoris published in Absil et al. (2013) obtained using the Annular Groove Phase Mask (AGPM) Vortex coronagraph. The sequence has been heavily sub-sampled temporarily to make it
smaller. The frames were also cropped to the central 101x101 area. In case you want to plug-in your cube just change the path of the following cells.
More info on this dataset, and on opening and visualizing fits files with VIP in general, is available in Tutorial 1. Quick start.
Let’s load the data:
[3]:
from vip_hci.fits import open_fits
psfnaco = '../datasets/naco_betapic_psf.fits'
cubename = '../datasets/naco_betapic_cube_cen.fits'
angname = '../datasets/naco_betapic_pa.fits'
cube = open_fits(cubename)
psf = open_fits(psfnaco)
angs = open_fits(angname)
FITS HDU-0 data successfully loaded. Data shape: (61, 101, 101)
FITS HDU-0 data successfully loaded. Data shape: (39, 39)
FITS HDU-0 data successfully loaded. Data shape: (61,)
Let’s fit the PSF with a 2D Gaussian to infer the FWHM, the flux in a 1-FWHM size aperture, and get a flux-normalized PSF:
[4]:
%matplotlib inline
from vip_hci.fm import normalize_psf
psfn, flux, fwhm_naco = normalize_psf(psf, size=19, debug=True, full_output=True)
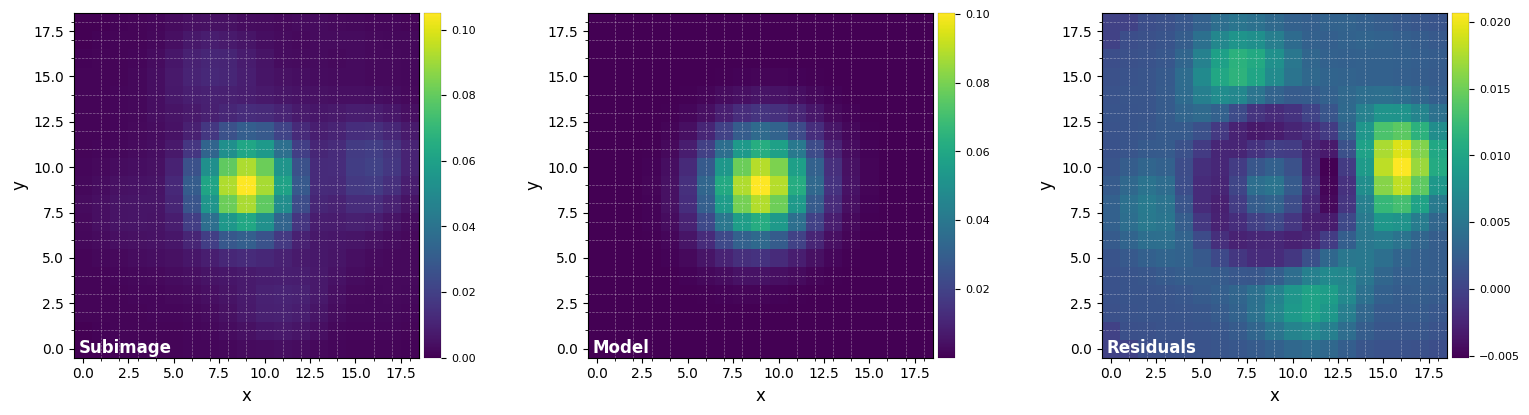
FWHM_y = 4.926059872957138
FWHM_x = 4.675778895005929
centroid y = 9.010992107833063
centroid x = 9.01917912265807
centroid y subim = 9.010992107833063
centroid x subim = 9.01917912265807
amplitude = 0.10032285220380603
theta = -38.446187060503874
Mean FWHM: 4.801
Flux in 1xFWHM aperture: 1.307
[5]:
print(fwhm_naco)
4.800919383981533
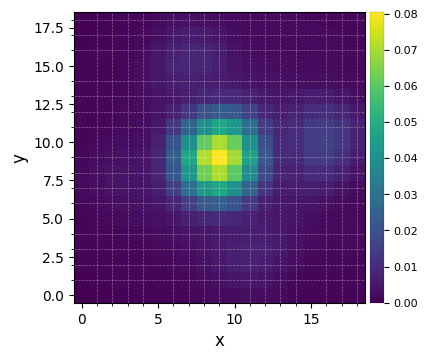
Let’s visualize the flux-normalized PSF:
[6]:
plot_frames(psfn, grid=True, size_factor=4)
Let’s finally define the pixel scale for NACO (L’ band), which we get from a dictionary stored in the config subpackage:
[7]:
from vip_hci.config import VLT_NACO
pxscale_naco = VLT_NACO['plsc']
print(pxscale_naco, "arcsec/px")
0.02719 arcsec/px
4.2. Signal-to-noise ratio and significance
4.2.1. S/N map
When testing different stellar PSF modeling and subtraction algorithms, one may end up with a point-like source in the final post-processing images. How can its signal-to-noise ratio be assessed?
By default we adopt the definition of S/N given in Mawet el al. (2014), which uses a two samples t-test for the problem of planet detection. Student (t) statistics are relevant for hypothesis testing in presence of a small sample, which is the case of high contrast imaging of point sources at small angles. Since the structure of speckle noise varies radially, only a limited sample of pixels, and independent apertures encompassing them, is available for noise estimation at each radius.
The main idea is to test the flux of a given speckle or planet candidate against the flux measured in independent apertures (resolution elements) at the same radial separation from the center:
where \(\overline{x}_1\) is the flux of the tested resolution element (blue dot in the figure below), \(\overline{x}_2\) and \(s_2\) are the mean and empirical standard deviation of the fluxes of the noise resolution elements (red dots in the figure below) and \(n_2\) the number of such noise resolution elements.
Let’s illustrate this process on a PCA post-processed image which contains a companion candidate:
[8]:
from vip_hci.psfsub import pca
pca_img = pca(cube, angs, ncomp=6, verbose=False, imlib='vip-fft', interpolation=None)
[9]:
%matplotlib inline
plot_frames(pca_img, grid=True)
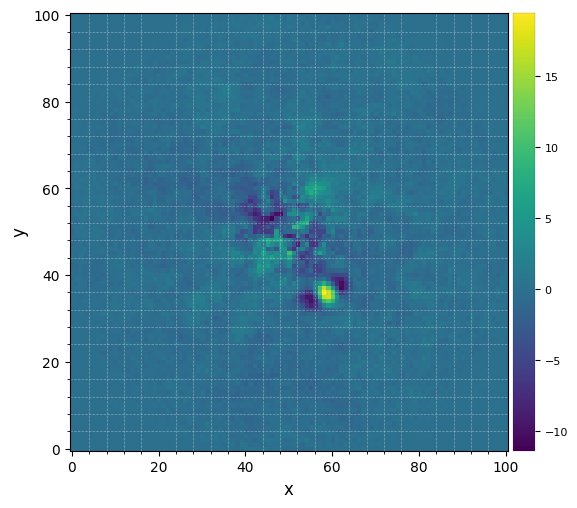
Let’s define the coordinates of a test point source in the image:
[10]:
xy_b = (58.8,35.3)
The snr function in the metrics module can be used to estimate the S/N ratio of the point source:
[11]:
from vip_hci.metrics import snr
snr1 = snr(pca_img, source_xy=xy_b, fwhm=fwhm_naco, plot=True)
snr1

[11]:
7.193726950870574
The S/N is relatively high, however we see that two of the test apertures are overlapping with the two negative side lobes (which is the typical signature for a point-source imaged with ADI). The exclude_negative_lobes option can be set to avoid considering apertures right next to the test aperture, which can make a significant difference in terms of S/N ratio in some cases:
[12]:
snr1 = snr(pca_img, source_xy=xy_b, fwhm=fwhm_naco, plot=True, exclude_negative_lobes=True)
snr1
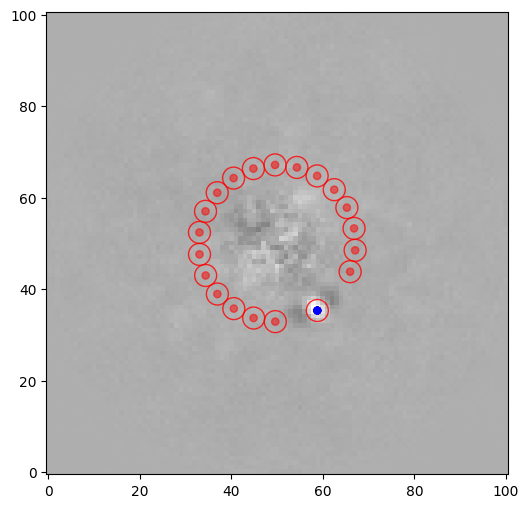
[12]:
14.27578045305458
One has to be careful with the exclude_negative_lobes option though, as it decreases the number of test apertures, hence increases the small-angle penalty factor.
In the metrics subpackage we have also implemented a function for S/N map generation, by computing the S/N for each pixel of a 2D array. It has a parameter nproc for exploiting multi-CPU systems which by default is None, meaning that it will use half the number of available CPUs in the system.
[13]:
from vip_hci.metrics import snrmap
snrmap_1 = snrmap(pca_img, fwhm=fwhm_naco, plot=True, nproc=None)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 10:48:54
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
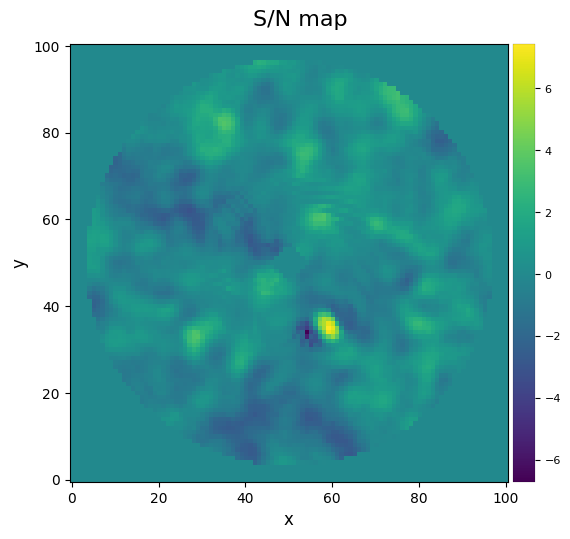
S/N map created using 5 processes
Running time: 0:00:03.025867
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
In case we really need the S/N map of a big frame (which can take quite some time to compute depending on your hardware), a good option is to use the approximated=True option. It uses an approximated S/N definition that yields close results to the one mentioned earlier.
[14]:
snrmap_f = snrmap(pca_img, fwhm=fwhm_naco, plot=True, approximated=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 10:48:57
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
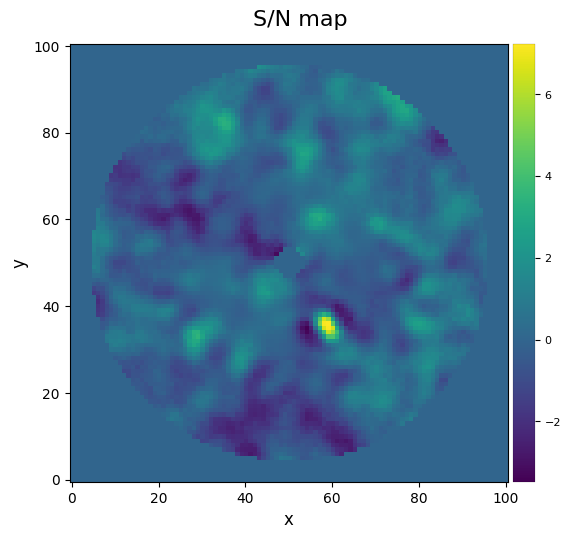
S/N map created using 5 processes
Running time: 0:00:00.325935
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Question 4.1: In the presence of azimuthally extended disc signals in the field of view, how do you expect the S/N ratio of authentic sources to behave? Would the classical definition above still be reliable, or would it underestimate/overestimate the true S/N ratio of authentic circumstellar signals?
4.2.2. Significance
Due to the common confusion between S/N ratio and significance, we have included a routine to convert (Student) S/N ratio (as defined above) into a Gaussian “sigma” significance, which is the most common metrics used to assess significance in signal detection theory.
The conversion is based on matching the false positive fraction (FPF; e.g. \(3 \times 10^{-7}\) for a \(5\sigma\) detection threshold), or equivalently the confidence level CL = 1-FPF.
As an example, let’s consider a second tentative source (arguably point-like) in our Beta Pic dataset:
[15]:
xy_test = (55.6, 59.7)
snr2 = snr(pca_img, source_xy=xy_test, fwhm=fwhm_naco, plot=True, exclude_negative_lobes=True)
print(snr2)

3.067524707858972
The first point source (as shown in Sec. 4.2.1.) has a very high S/N of ~13.8. The second point-like source has a S/N ~3.1. What is the significance level that each blob is an authentic point source detection (i.e. not a residual speckle emerging randomly as part of the residual intensity distribution)?
The significance routine in the metrics module takes into account both the S/N ratio and the radial separation of the point source (the FWHM is also required to express that radial separation in terms of FWHM), for conversion to significance in terms of Gaussian statistics.
[16]:
from vip_hci.metrics import significance
from vip_hci.var import frame_center
cy, cx = frame_center(cube[0])
rad1 = np.sqrt((cy-xy_b[1])**2+(cx-xy_b[0])**2)
rad2 = np.sqrt((cy-xy_test[1])**2+(cx-xy_test[0])**2)
sig1 = significance(snr1, rad1, fwhm_naco, student_to_gauss=True)
sig2 = significance(snr2, rad2, fwhm_naco, student_to_gauss=True)
msg = "The point-like signal with S/N={:.1f} at r = {:.1f}px ({:.1f} FWHM radius) corresponds to a {:.1f}-sigma detection (Gaussian statistics)."
print(msg.format(snr1, rad1, rad1/fwhm_naco, sig1))
print(msg.format(snr2, rad2, rad2/fwhm_naco, sig2))
At a separation of 17.1 px (3.6 FWHM), S/N = 14.3 corresponds to a 6.9-sigma detection in terms of Gaussian false alarm probability.
At a separation of 11.2 px (2.3 FWHM), S/N = 3.1 corresponds to a 2.6-sigma detection in terms of Gaussian false alarm probability.
The point-like signal with S/N=14.3 at r = 17.1px (3.6 FWHM radius) corresponds to a 6.9-sigma detection (Gaussian statistics).
The point-like signal with S/N=3.1 at r = 11.2px (2.3 FWHM radius) corresponds to a 2.6-sigma detection (Gaussian statistics).
The first point-like signal appears to be an authentic circumstellar point source (i.e. a physical companion or background object) given that its confidence level is equivalent to that of a \(6.9\sigma\) detection (Gaussian sigma). For the second blob, the confidence level is equivalent to that of a \(2.7\sigma\) detection (Gaussian statistics) - i.e. it is not a significant detection considering common conventions (3-sigma or 5-sigma threhold).
Question 4.2: How can one disentangle a physically bound companion (planet, brown dwarf of stellar binary) from a background object?
4.2.3. STIM map
In the presence of extended disc signals, an alternative to the S/N map is to use the Standardized Trajectory Intensity Map (STIM; Pairet et al. 2019). A comparison between S/N and STIM maps for disc signals in the system of PDS 70 can be found in Christiaens et al. (2019a).
The STIM map is defined by:
where \(\mu_z\) and \(\sigma_z\) are the temporal mean and standard deviation of the derotated residual cube across the temporal dimension, respectively. It is calculated for each pixel (x,y).
Let’s calculate it for our Beta Pictoris L’-band test dataset. For that, let’s first run PCA with full_output=True to also return the residual cube and derotated residual cube:
[17]:
from vip_hci.metrics import stim_map
pca_img, _,_, pca_res, pca_res_der = pca(cube, angs, ncomp=15, verbose=False, full_output=True,
imlib='skimage', interpolation='biquartic')
stim_map = stim_map(pca_res_der)
In order to assess which signals are significant in the STIM map, Pairet et al. (2019) recommend to normalize the STIM map with the maximum intensity found in the inverse STIM map, which is obtained in a same way as the STIM map but using opposite angles for the derotation of the residual cube. Starting from VIP v1.6.0, this can be done with function normalized_stim_map. For previous versions, this involves the use of inverse_stim_map:
[18]:
from vip_hci.metrics import inverse_stim_map
inv_stim_map = inverse_stim_map(pca_res, angs)
if version.parse(vvip) < version.parse("1.6.0"):
norm_stim_map = stim_map/np.nanmax(inv_stim_map)
else:
from vip_hci.metrics import normalized_stim_map
norm_stim_map = normalized_stim_map(pca_res, angs)
Using the exact opposite values of derotation angles leads to a similar structure for the residual speckle noise, while authentic signals are not expected to sum up constructively. Therefore the maximum value in the inverse STIM map gives a good estimate of the maximum STIM intensity that one would expect from noise alone.
[19]:
plot_frames((stim_map, inv_stim_map, norm_stim_map), grid=True,
label=('STIM map', 'inv. STIM map', 'norm. STIM map'))
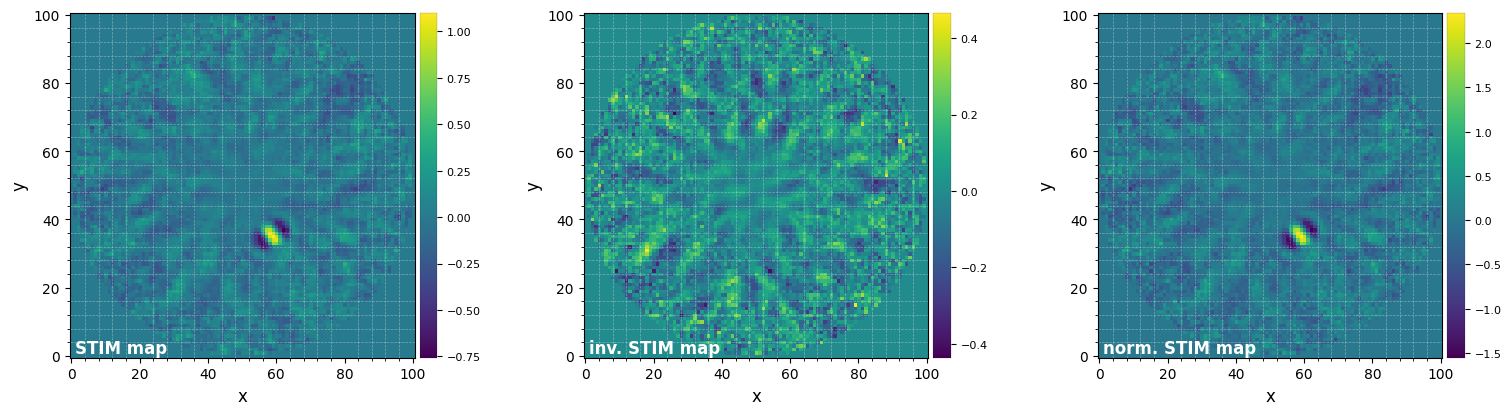
Any value larger than unity in the normalized STIM map is therefore expected to be significant. This can be visualized by thresholding the normalized STIM map.
[20]:
thr_stim_map = norm_stim_map.copy()
thr_stim_map[np.where(thr_stim_map<1)]=0
Beta Pic b is considered significant with the above criterion, although no extended disc structure is detected:
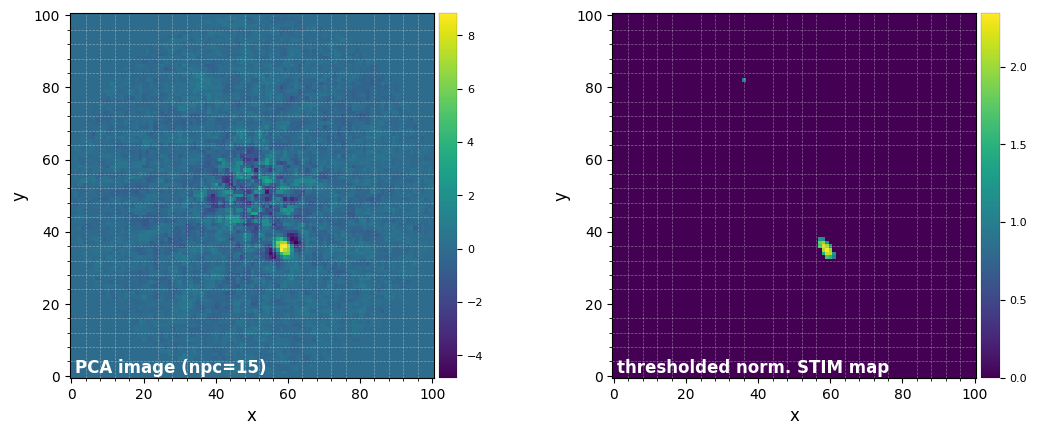
[21]:
plot_frames((pca_img, thr_stim_map), grid=True,
label=('PCA image (npc=15)', 'thresholded norm. STIM map'))
Answer 4.1: When test apertures include disc signal, the mean flux \(\bar{x}_2\) will be higher and/or the noise level will be overestimated (if the extended signal does not cover all apertures), hence leading in both cases to an underestimated S/N ratio of authentic disc signals. The above definition is therefore only relevant for point source detection.
Answer 4.2: With enough follow-up observations one can monitor the relative astrometry of the companion candidate with respect to the star, and compare it to the proper motion of the star (typically known to good precision thanks to Gaia for nearby stars). A background object (much further away) is expected to have a significantly different (typically much smaller) proper motion than the target. In absence of follow-up observations, a first statistical argument can be made based on the
separation of the companion candidate and the number density of background objects in that area of the sky - this can be estimated with VIP’s vip.stats.bkg_star_proba routine combined with the help of a Galactic model (e.g. TRILEGAL or Besançon model).
4.3. Automatic detection function
The frame_report routine provides some basic statistics about any post-processed image, including the position and SNR of any candidate in the image. Let’s try it on the median-ADI image obtained on our toy dataset:
[22]:
from vip_hci.psfsub import median_sub
fr_adi = median_sub(cube, angs)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 10:49:06
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Median psf reference subtracted
Done derotating and combining
Running time: 0:00:02.603378
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
[23]:
from vip_hci.metrics import frame_report
frame_report(fr_adi, fwhm=fwhm_naco)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 10:49:09
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
S/N map created using 5 processes
Running time: 0:00:02.810041
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Coords of Max px (X,Y) = 55.0, 54.0
Flux in a centered 1xFWHM circular aperture = 470.077
Central pixel S/N = 3.561
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Inside a centered 1xFWHM circular aperture:
Mean S/N (shifting the aperture center) = 1.667
Max S/N (shifting the aperture center) = 3.561
stddev S/N (shifting the aperture center) = 1.012
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
[23]:
((55, 54), [470.07687891671645], [3.5612234828789724], 1.6674225229822748)
Let’s try the detection function in the metrics module. This is a computer vision blob-detection method based on the Laplacian of Gaussian filter (http://scikit-image.org/docs/dev/api/skimage.feature.html#skimage.feature.blob_log).
Provided a post-processed frame, the FWHM in pixels and a PSF (i.e. what a planet should look like), this function can return the position of point-like sources in the image. Take a look at the help/docstring for a detailed explanation of the function. Depending on the mode the results can be different. A S/N minimum criterion can be provided with snr_thresh.
Let’s try it on the median-ADI and annular PCA images obtained on the Beta Pic b dataset:
[24]:
from vip_hci.metrics import detection
detection(fr_adi, fwhm=fwhm_naco, psf=psfn, debug=False, mode='log', snr_thresh=5,
bkg_sigma=5, matched_filter=False)
Blobs found: 3
ycen xcen
------ ------
46.130 43.396
35.555 58.654
57.920 47.674
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (43.4,46.1)
S/N constraint NOT fulfilled (S/N = 1.626)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (58.7,35.6)
S/N constraint NOT fulfilled (S/N = 2.552)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (47.7,57.9)
S/N constraint NOT fulfilled (S/N = 0.797)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
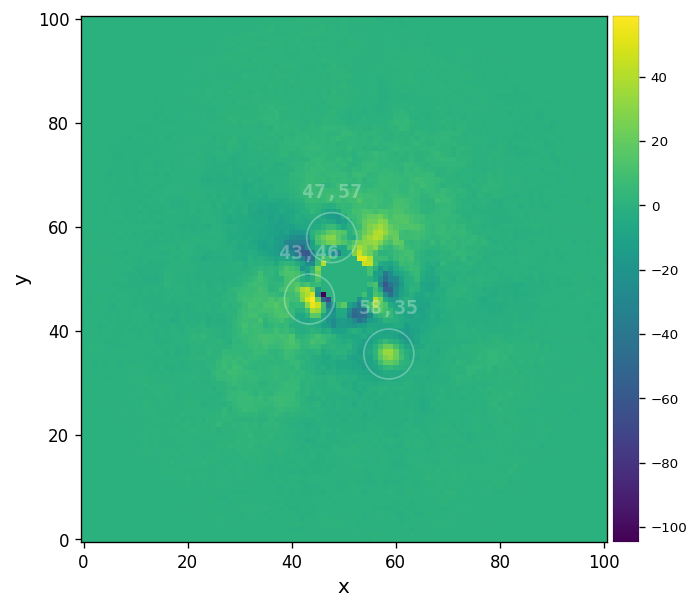
[24]:
(array([], dtype=float64), array([], dtype=float64))
Planet b is highlighted but with rather small S/N (~2). We note that a number of other much less convicing blobs are also highlighted. Let’s try the frame obtained with annular PCA:
[25]:
from vip_hci.psfsub import pca_annular
fr_pca = pca_annular(cube, angs, ncomp=7)
detection(fr_pca, fwhm=fwhm_naco, psf=psfn, bkg_sigma=5, debug=False, mode='log',
snr_thresh=5, plot=True, verbose=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 10:49:12
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
N annuli = 12, FWHM = 4.000
PCA per annulus (or annular sectors):
Ann 1 PA thresh: 11.42 Ann center: 2 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.081019
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 2 PA thresh: 6.94 Ann center: 6 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.127425
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 3 PA thresh: 6.04 Ann center: 10 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.235318
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 4 PA thresh: 5.65 Ann center: 14 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.352334
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 5 PA thresh: 5.44 Ann center: 18 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.460634
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 6 PA thresh: 5.30 Ann center: 22 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.626957
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 7 PA thresh: 5.21 Ann center: 26 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.797973
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 8 PA thresh: 5.14 Ann center: 30 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:00.983263
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 9 PA thresh: 5.08 Ann center: 34 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:00:01.190271
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 10 PA thresh: 5.04 Ann center: 38 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:17:41.981366
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 11 PA thresh: 5.01 Ann center: 42 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:17:43.169872
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Ann 12 PA thresh: 5.09 Ann center: 45 N segments: 1
Done PCA with lapack for current annulus
Running time: 0:17:43.380898
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Done derotating and combining.
Running time: 0:17:45.858609
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Blobs found: 4
ycen xcen
------ ------
35.703 58.491
58.856 55.039
45.943 55.871
44.344 48.461
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (58.5,35.7)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Coords of chosen px (X,Y) = 58.5, 35.7
Flux in a centered 1xFWHM circular aperture = 375.747
Central pixel S/N = 9.561
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Inside a centered 1xFWHM circular aperture:
Mean S/N (shifting the aperture center) = 8.255
Max S/N (shifting the aperture center) = 9.809
stddev S/N (shifting the aperture center) = 1.326
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (55.0,58.9)
S/N constraint NOT fulfilled (S/N = 3.253)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (55.9,45.9)
S/N constraint NOT fulfilled (S/N = 1.476)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
X,Y = (48.5,44.3)
S/N constraint NOT fulfilled (S/N = 2.083)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
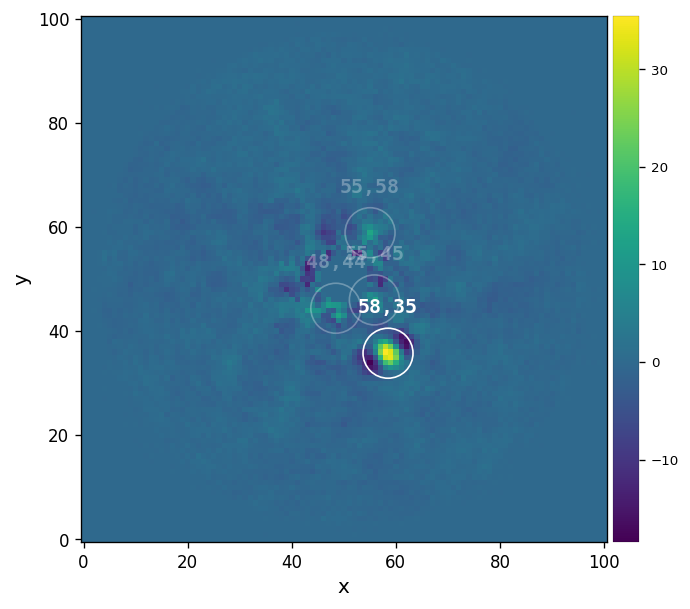
[25]:
(array([35.70251528]), array([58.49135008]))
We see that only one point-like source stands out above the SNR=5 threshold (set with snr_thresh): beta Pic b.
We see from these tests that one should take the results obtained by this automatic detection algorithm with a pinch of salt (see. e.g the signals at the edge of the inner mask). It is unlikely to detect point sources better then can be inferred from visual inspection by human eyes. Much more advanced machine learning techniques should be used to infer the presence of companions that cannot be detected from visual inspection of the final image, and with low false positive fraction (see e.g. Gomez Gonzalez et al. 2018 or Cantero et al. 2023).
4.4. Throughput and contrast curves
4.4.1. Throughput
VIP allows to measure the throughput of its algorithms by injecting fake companions. The throughput gives us an idea of how much the algorithm subtracts or biases the signal from companions, as a function of the distance from the center (high throughput = low amount of self-subtraction). Let’s assess it for our toy datacube. The relevant function is throughput in the metrics module.
In order to measure reliable throughput and contrast curves, one first need to subtract from the data all real companions.
We’ll see in Tutorial 5. how to obtain reliable estimates on the parameters of directly imaged companions (radial separation, azimuth and flux). Let’s assume we have inferred these parameters. It is only a matter of calling the cube_planet_free function in the fm module:
[26]:
from vip_hci.fm import cube_planet_free
r_b = 0.452/pxscale_naco # Absil et al. (2013)
theta_b = 211.2+90 # Absil et al. (2013)
f_b = 648.2
cube_emp = cube_planet_free([(r_b, theta_b, f_b)], cube, angs, psfn=psfn)
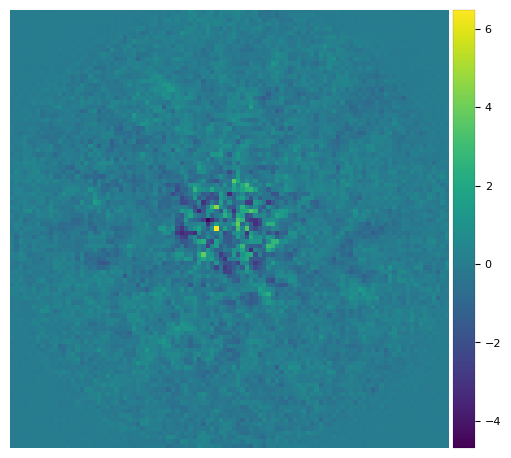
Let’s double check the planet was efficiently removed:
[27]:
pca_emp = pca(cube_emp, angs, ncomp=12, verbose=False)
plot_frames(pca_emp, axis=False)
Let’s now compute the throughput with the empty cube:
[28]:
from vip_hci.metrics import throughput
res_thr = throughput(cube_emp, angs, psfn, fwhm_naco, ncomp=15,
algo=pca, nbranch=1, full_output=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:22:09
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Cube without fake companions processed with pca
Running time: 0:00:03.414676
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Measured annulus-wise noise in resulting frame
Running time: 0:00:03.536397
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Flux in 1xFWHM aperture: 1.000
Fake companions injected in branch 1 (pattern 1/3)
Running time: 0:00:03.712720
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Cube with fake companions processed with pca
Measuring its annulus-wise throughput
Running time: 0:00:06.914992
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Fake companions injected in branch 1 (pattern 2/3)
Running time: 0:00:07.021930
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Cube with fake companions processed with pca
Measuring its annulus-wise throughput
Running time: 0:00:09.902454
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Fake companions injected in branch 1 (pattern 3/3)
Running time: 0:00:10.026218
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Cube with fake companions processed with pca
Measuring its annulus-wise throughput
Running time: 0:00:12.554494
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Finished measuring the throughput in 1 branches
Running time: 0:00:12.566565
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
[29]:
plt.figure(figsize=(6,3))
plt.plot(res_thr[3], res_thr[0][0,:], 'o-', alpha=0.5)
plt.ylabel('throughput')
plt.xlabel('separation in pixels')
[29]:
Text(0.5, 0, 'separation in pixels')
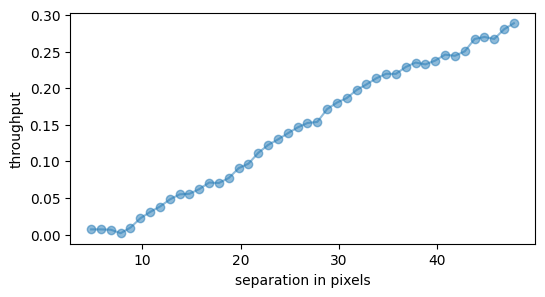
Question 4.3: Why does the throughput increase with radial separation?
Let’s compare this with the annular PCA result:
[30]:
res_thr2 = throughput(cube_emp, angs, psfn, fwhm_naco, algo=pca_annular, nbranch=1, verbose=False,
full_output=True, ncomp=10, radius_int=int(fwhm_naco),
delta_rot=0.5, asize=fwhm_naco)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:22:22
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:22:26
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:22:31
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:22:34
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
[31]:
plt.figure(figsize=(6,3))
plt.plot(res_thr[3], res_thr[0][0,:], 'o-', label='PCA', alpha=0.5)
plt.plot(res_thr2[3], res_thr2[0][0,:], 'o-', label='annular PCA', alpha=0.5)
plt.ylabel('throughput')
plt.xlabel('separation in pixels')
_ = plt.legend(loc='best')
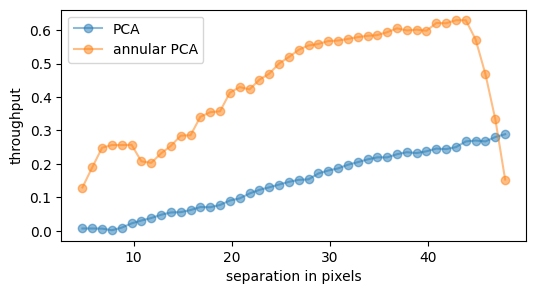
We clearly see the gain in throughput by applying a parallactic angle rejection in our annular PCA processing. For a sequence with more field rotation, the delta_rot value could be increased to further increase the throughput. Note that the drop to zero at the end is due to incomplete padding of the field with concentric annuli.
Answer 4.3: For a given parallactic angle threshold (or lack thereof in standard pca.pca), there is more linear motion of the field radially outward, resulting in less self-subtraction of any putative planet.
4.4.2. Contrast curves
Now let’s see how to generate 5-sigma contrast curves for ADI data using the contrast_curve function. The contrast curve shows the achieved contrast (i.e. how much fainter than the star a companion can be detected) as a function of radius, for a given datacube post-processed with a given algorithm.
The contrast curve takes into account both the noise level in the final image and the algorithmic throughput (previous subsection). The noise level is used to infer the signal required for the S/N to achieve a 5-sigma significance at each radial separation, as calculated in Section 4.2.2. Note that sigma is an input parameter such that the contrast curve can also be calculated for e.g. 1 or 3 \(\sigma\). Let’s set it to 5:
[32]:
nsig=5
Among other parameters of the contrast_curve function, algo takes any function in VIP for model PSF subtraction, and optional parameters of the algo can also be passed as regular parameters of contrast_curve. Parameter starphot sets the flux of the star. The latter was obtained from the non-coronagraphic PSF before normalization and after rescaling to the integration time used in the coronagraphic observations:
[33]:
starphot = 764939.6
In the example below, we’ll first calculate the contrast curve obtained with full-frame PCA, and then with PCA in concentric annuli with a PA threshold.
[34]:
from vip_hci.metrics import contrast_curve
cc_1 = contrast_curve(cube_emp, angs, psfn, fwhm=fwhm_naco, pxscale=pxscale_naco, starphot=starphot,
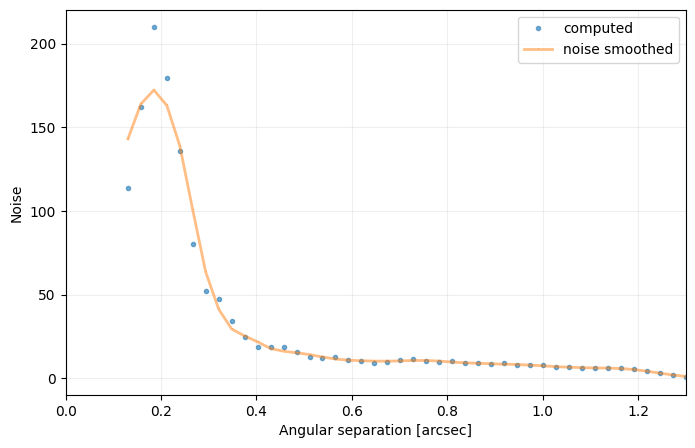
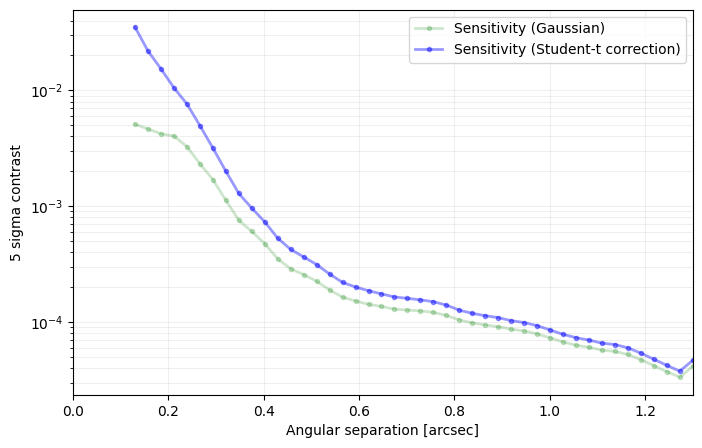
sigma=nsig, nbranch=3, algo=pca, ncomp=9, debug=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:22:38
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
ALGO : pca, FWHM = 4.800919383981533, # BRANCHES = 3, SIGMA = 5, STARPHOT = 764939.6
Finished the throughput calculation
Running time: 0:00:21.479786
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
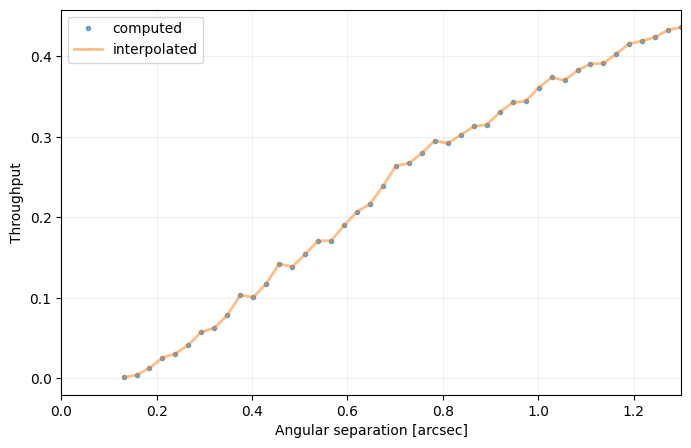
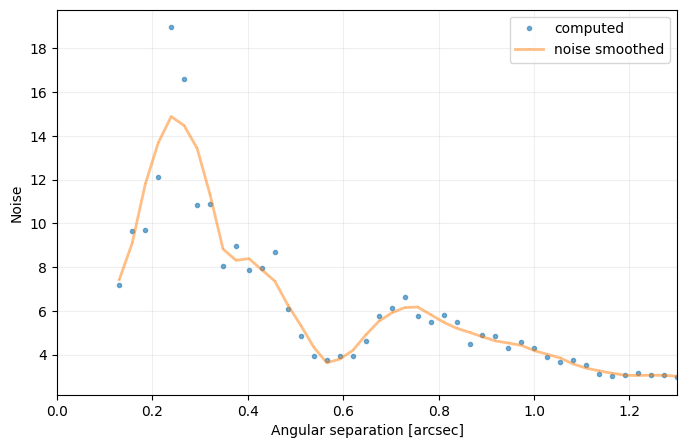
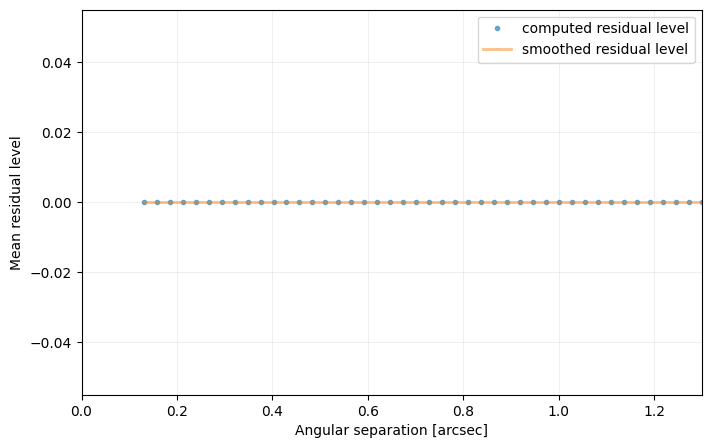
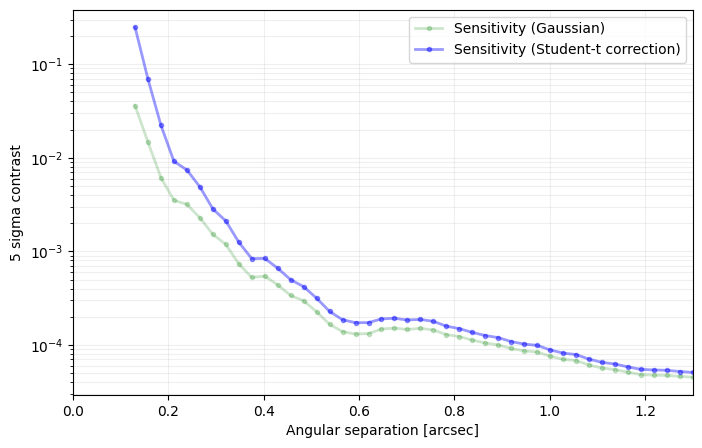
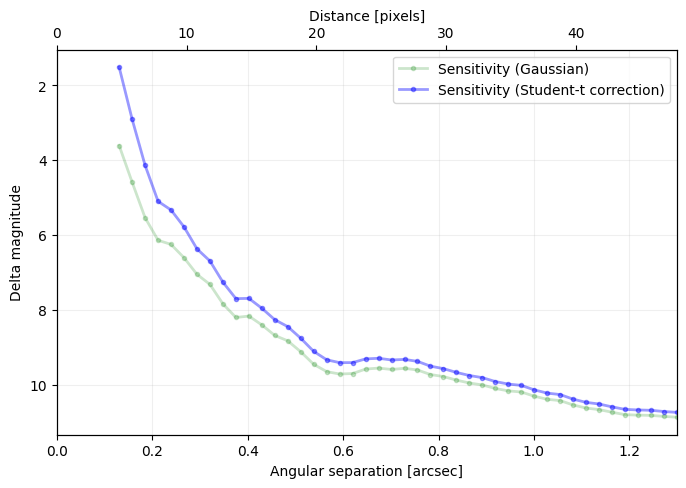
[35]:
cc_2 = contrast_curve(cube_emp, angs, psfn, fwhm=fwhm_naco, pxscale=pxscale_naco, starphot=starphot,
sigma=nsig, nbranch=1, delta_rot=0.5, algo=pca_annular, ncomp=8,
radius_int=int(fwhm_naco), asize=fwhm_naco, debug=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:00
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
ALGO : pca_annular, FWHM = 4.800919383981533, # BRANCHES = 1, SIGMA = 5, STARPHOT = 764939.6
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:00
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:03
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:07
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:10
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Finished the throughput calculation
Running time: 0:00:13.194970
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
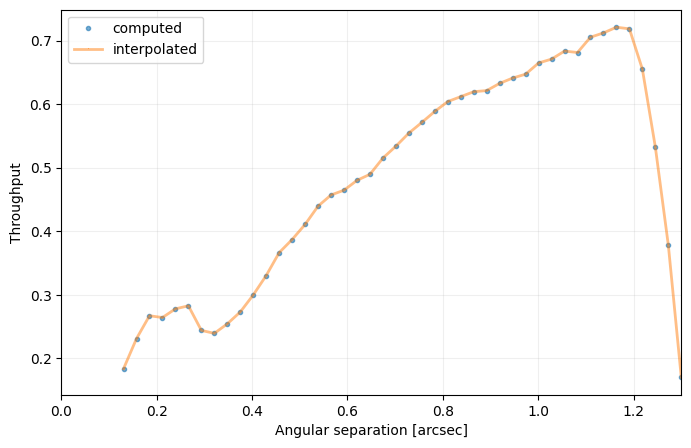
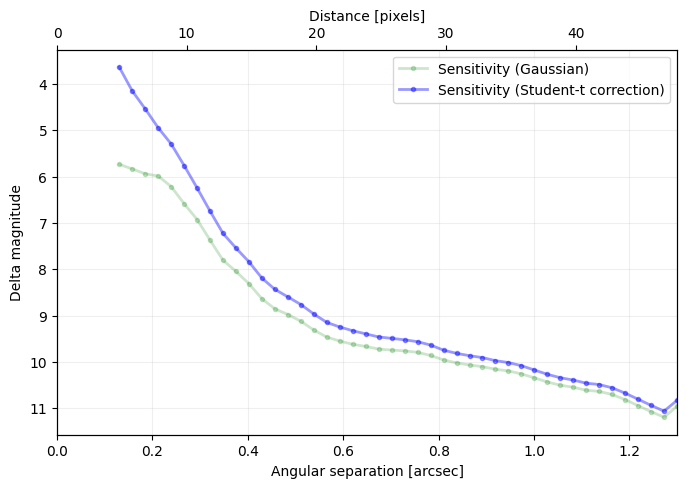
Question 4.4: Considering the hard encoded planet parameters and stellar flux provided above, where would Beta Pic b sit in this contrast curve?
Question 4.5: If a companion is present in the datacube, how do you expect it to affect the contrast curve? In other words what would happen if cube was provided to contrast_curve instead of cube_emp?
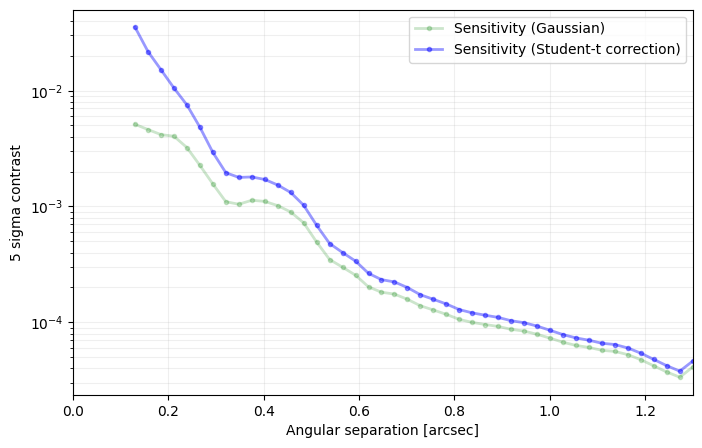
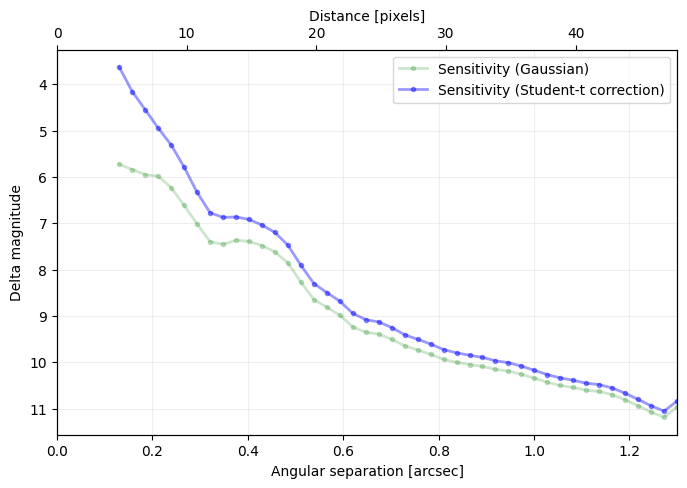
Answer 4.4: As illustrated below.
[36]:
plt.figure(figsize=(8,5))
plt.plot(cc_1['distance']*pxscale_naco,
-2.5*np.log10(cc_1['sensitivity_student']),
'r-', label='{}-sigma contrast (PCA)'.format(nsig), alpha=0.5)
plt.plot(cc_2['distance']*pxscale_naco,
-2.5*np.log10(cc_2['sensitivity_student']),
'b-', label='{}-sigma contrast (annular PCA)'.format(nsig), alpha=0.5)
r_b = 16.583
plt.plot(r_b*pxscale_naco,
-2.5*np.log10(700./starphot), 'gs', label='Beta Pic b')
plt.gca().invert_yaxis()
plt.ylabel('Contrast (mag)')
plt.xlabel('Separation (arcsec)')
_ = plt.legend(loc='best')
plt.show()
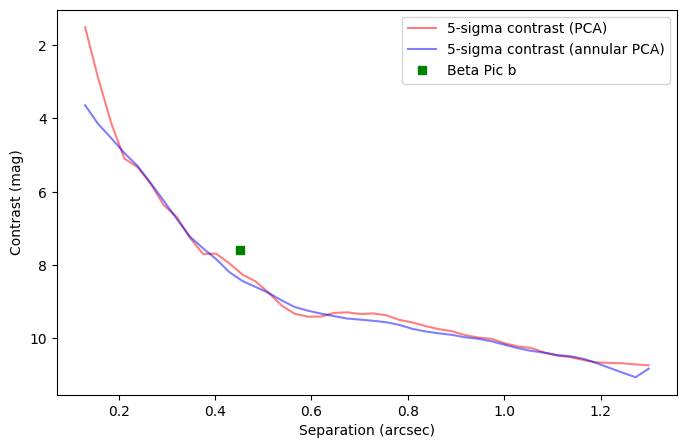
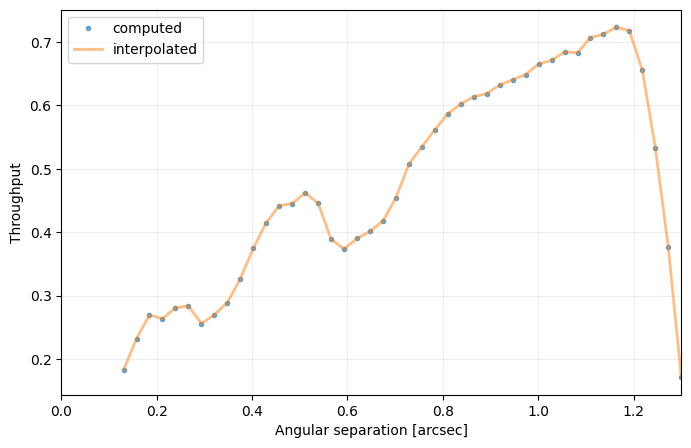
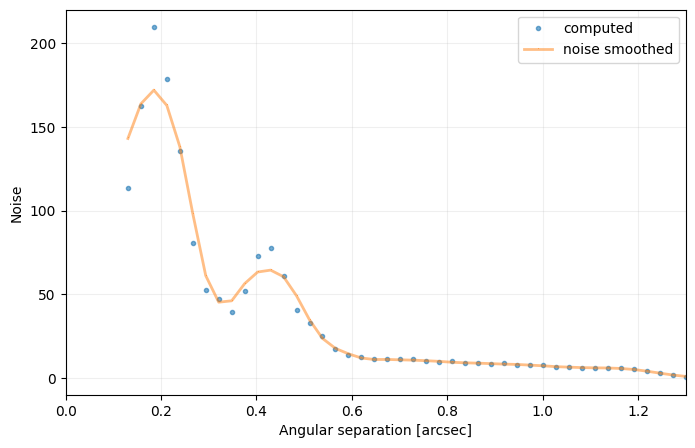
Answer 4.5: It would artificially increase the estimated contrast at the radial separation of the companion (creating a bump in the curve) - as it would be considered as extra noise. Illustration below:
[37]:
cc_not_emp = contrast_curve(cube, angs, psfn, fwhm=fwhm_naco, pxscale=pxscale_naco, starphot=starphot,
sigma=nsig, nbranch=1, delta_rot=0.5, algo=pca_annular, ncomp=8,
radius_int=int(fwhm_naco), asize=fwhm_naco, debug=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:14
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
ALGO : pca_annular, FWHM = 4.800919383981533, # BRANCHES = 1, SIGMA = 5, STARPHOT = 764939.6
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:14
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:17
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:21
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-28 11:23:27
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Finished the throughput calculation
Running time: 0:00:17.594471
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
4.5. Completeness curves and maps
4.5.1. Completeness curves
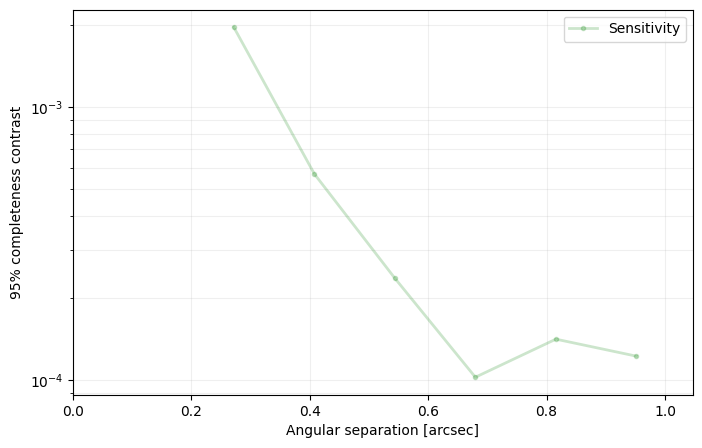
VIP allows the calculation of completeness curves, as implemented in Dahlqvist et al. (2021) following the framework introduced in Jensen-Clem et al. (2018).
These are contrast curves corresponding to a given completeness level (e.g. 95%) and one false positive in the full frame. In other words, the 95% completeness curve corresponds to the contrast at which a given companion would be recovered 95% of the time (19/20 true positives).
Setting an_dist to None produces a contrast curve spanning 2 FWHM in radius to half the size of the provided cube images minus half of the PSF frame, with a step of 5 pixels.
[38]:
# let's first crop the PSF image
from vip_hci.preproc import frame_crop
crop_sz = 15
if psfn.shape[-1]>crop_sz:
psfn = frame_crop(psfn, crop_sz)
New shape: (15, 15)
[39]:
from vip_hci.metrics import completeness_curve
an_dist, comp_curve = completeness_curve(cube_emp, angs, psfn, fwhm_naco, pca, an_dist=np.arange(10,40,5),
pxscale=pxscale_naco, ini_contrast = 1e-3/np.arange(10,40,5), starphot=starphot,
plot=True, nproc=None, algo_dict={'ncomp':5, 'imlib':'opencv'})
Calculating initial SNR map with no injected companion...
*** Calculating contrast at r = 10 ***
Found contrast level for first TP detection: 0.00050625
Found lower and upper bounds of sought contrast: [0.0017085937499999998, 0.0025628906249999996]
=> found final contrast for 95.0% completeness: 0.00196171875
*** Calculating contrast at r = 15 ***
Found contrast level for first TP detection: 0.00022500000000000002
Found lower and upper bounds of sought contrast: [0.00050625, 0.000759375]
=> found final contrast for 95.0% completeness: 0.0005695312499999999
*** Calculating contrast at r = 20 ***
Found contrast level for first TP detection: 0.00011250000000000001
Found lower and upper bounds of sought contrast: [0.00016875, 0.000253125]
=> found final contrast for 95.0% completeness: 0.00023625
*** Calculating contrast at r = 25 ***
Found contrast level for first TP detection: 4e-05
Found lower and upper bounds of sought contrast: [9.000000000000002e-05, 0.00013500000000000003]
=> found final contrast for 95.0% completeness: 0.00010253376000000003
*** Calculating contrast at r = 30 ***
Found contrast level for first TP detection: 5e-05
Found lower and upper bounds of sought contrast: [0.00011250000000000001, 0.00016875]
=> found final contrast for 95.0% completeness: 0.00014135112762451174
*** Calculating contrast at r = 35 ***
Found contrast level for first TP detection: 6.428571428571429e-05
Found lower and upper bounds of sought contrast: [9.642857142857143e-05, 0.00014464285714285715]
=> found final contrast for 95.0% completeness: 0.00012245344201820667
4.5.2. Completeness maps
One can also compute completeness maps, considering the dependency of the contrast on both radius and completeness. Since this is a very slow process (even slower than the completeness curve), we will limit it to only one of the radii tested for the completeness curves, and set the initial contrast (ini_contrast) to the output of the completeness_curve function at that radius:
[40]:
n_fc = 20
test_an_dist = 25 # tested radial distance
# initial contrast set to value found in completeness curve
idx = np.where(an_dist == test_an_dist)[0]
ini_contrast = comp_curve[idx]
[41]:
from vip_hci.metrics import completeness_map
an_dist, comp_levels, contrasts = completeness_map(cube_emp, angs, psfn, fwhm_naco, pca, an_dist=[test_an_dist],
n_fc=n_fc, ini_contrast=ini_contrast, starphot=starphot,
nproc=None, algo_dict={'ncomp':3, 'imlib':'opencv'})
Starting annulus 25
Lower bound (5%) found: 1.3686604804687503e-05
Upper bound (95%) found: 0.00020026125000000006
Data point 0.15 found. Still 13 data point(s) missing
Data point 0.25 found. Still 12 data point(s) missing
Data point 0.3 found. Still 10 data point(s) missing
Data point 0.4 found. Still 9 data point(s) missing
Data point 0.5 found. Still 8 data point(s) missing
Data point 0.55 found. Still 7 data point(s) missing
Data point 0.6 found. Still 6 data point(s) missing
Data point 0.7 found. Still 5 data point(s) missing
Data point 0.75 found. Still 4 data point(s) missing
Data point 0.8 found. Still 2 data point(s) missing
Data point 0.85 found. Still 1 data point(s) missing
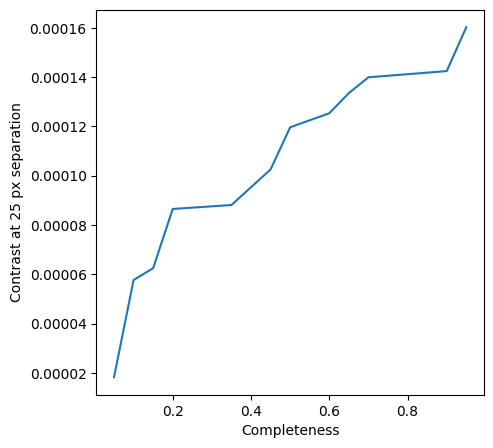
Let’s plot the achieved contrast as a function of the assumed completeness ratio, at a radial separation of 25 px:
[42]:
fig = plt.figure(figsize = [5,5])
plt.plot(comp_levels, contrasts[0,:])
plt.xlabel("Completeness")
plt.ylabel("Contrast at {} px separation".format(test_an_dist))
plt.show()
4.6. Applefy contrast curves and grids
Applefy enables the calculation of robust detection limits, be it contrast curves or contrast grids, for different assumptions on the residual noise in the image (see details in Bonse et al. 2023). The package is not a mandatory requirement of VIP, but intercompatibility is possible with the pca algorithm (only option as of 31 August 2023, more algorithms may become
compatible later). Below are some example usages to calculate robust contrast curves and contrast grids if you have Applefy installed (see installation instructions here).
[43]:
try:
import applefy
applefy_installed=True
except:
applefy_installed=False
Let’s first define an Applefy Contrast instance for our dataset (using the cube where the planet was already removed), and a checkpoint directory where intermediate files will be saved (also enabling a faster re-calculation of the contrast curves later):
[44]:
checkpoint_dir = "../datasets/TMP/cc/"
[45]:
if applefy_installed:
from applefy.detections.contrast import Contrast
contrast_instance = Contrast(science_sequence=cube_emp, psf_template=psfn, parang_rad=angs,
psf_fwhm_radius=fwhm_naco/2, dit_psf_template=1., dit_science=starphot,
scaling_factor=1., # A factor to account e.g. for ND filters
checkpoint_dir=checkpoint_dir)
4.6.1. Applefy contrast curves
Let’s now define the brightness and number of fake planets to be injected:
[46]:
flux_ratio_mag = 7 # magnitude difference of injected fake planets
num_fake_planets = 6 # number of injected fake planets azimuthally
[47]:
if applefy_installed:
from applefy.utils import flux_ratio2mag, mag2flux_ratio
flux_ratio = mag2flux_ratio(flux_ratio_mag)
print("{} fake planets will be injected azimuthally at {} flux ratio ({:.1f} mag difference)".format(num_fake_planets,
flux_ratio,
flux_ratio_mag))
6 fake planets will be injected azimuthally at 0.001584893192461114 flux ratio (7.0 mag difference)
[48]:
if applefy_installed:
contrast_instance.design_fake_planet_experiments(flux_ratios=flux_ratio,
num_planets=num_fake_planets,
overwrite=True)
Overwriting existing config files.
Let’s now run the fake planet experiment. For this we consider a grid of tested numbers of principal components:
[49]:
if applefy_installed:
components = [1, 4, 8, 13, 19, 25, 32] # can also be a tuple of 3 elements with a given step
from applefy.wrappers.vip import MultiComponentPCAvip
algorithm_function = MultiComponentPCAvip(num_pcas=components, kwarg={'verbose':False})
contrast_instance.run_fake_planet_experiments(algorithm_function=algorithm_function,
num_parallel=cpu_count()//2)
Running fake planet experiments...
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 61/61 [02:53<00:00, 2.84s/it]
[DONE]
Select the aperture photometry mode (choice between spaced pixels “FS” or aperture sums “ASS”):
[50]:
if applefy_installed:
from applefy.utils.photometry import AperturePhotometryMode
# Use apertures pixel values
photometry_mode_planet = AperturePhotometryMode(
"ASS", # or "AS"
psf_fwhm_radius=fwhm_naco/2,
search_area=0.5)
photometry_mode_noise = AperturePhotometryMode(
"AS",
psf_fwhm_radius=fwhm_naco/2)
[51]:
if applefy_installed:
contrast_instance.prepare_contrast_results(
photometry_mode_planet=photometry_mode_planet,
photometry_mode_noise=photometry_mode_noise)
Select the statistical test to be used:
[52]:
if applefy_installed:
from applefy.statistics import TTest, gaussian_sigma_2_fpf, fpf_2_gaussian_sigma, LaplaceBootstrapTest
[53]:
if applefy_installed:
statistical_test = TTest()
Finally, let’s calculate the contrast curves (see all options in the Applefy tutorial)
[54]:
if applefy_installed:
contrast_curves, contrast_errors = contrast_instance.compute_analytic_contrast_curves(
statistical_test=statistical_test,
confidence_level_fpf=gaussian_sigma_2_fpf(5),
num_rot_iter=20,
pixel_scale=pxscale_naco)
Computing contrast curve for PCA (001 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.58it/s]
Computing contrast curve for PCA (004 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.69it/s]
Computing contrast curve for PCA (008 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.78it/s]
Computing contrast curve for PCA (013 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.77it/s]
Computing contrast curve for PCA (019 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.77it/s]
Computing contrast curve for PCA (025 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.75it/s]
Computing contrast curve for PCA (032 components)
100%|███████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 10/10 [00:02<00:00, 3.72it/s]
Let’s examine the output:
[55]:
if applefy_installed:
contrast_curves
Let’s now plot the contrast curves:
[56]:
if applefy_installed:
# compute the overall best contrast curve
overall_best = np.min(contrast_curves.values, axis=1)
[57]:
if applefy_installed:
# get the error bars of the the overall best contrast curve
best_idx = np.argmin(contrast_curves.values, axis=1)
best_contrast_errors = contrast_errors.values[np.arange(len(best_idx)), best_idx]
[58]:
if no_sns:
colors = ['b','c','g','y','orange','r','m','k']
else:
# nicer plotting if seaborn installed
colors = sns.color_palette("rocket_r",
n_colors=len(contrast_curves.columns))
colors.append('b')
[59]:
if applefy_installed:
separations_arcsec = contrast_curves.reset_index(level=0).index
separations_FWHM = contrast_curves.reset_index(level=1).index
[60]:
if applefy_installed:
# 1.) Create Plot Layout
fig = plt.figure(constrained_layout=False, figsize=(12, 8))
gs0 = fig.add_gridspec(1, 1)
axis_contrast_curvse = fig.add_subplot(gs0[0, 0])
# ---------------------- Create the Plot --------------------
i = 0 # color picker
for tmp_model in contrast_curves.columns:
num_components = int(tmp_model[5:9])
tmp_flux_ratios = contrast_curves.reset_index(
level=0)[tmp_model].values
tmp_errors = contrast_errors.reset_index(
level=0)[tmp_model].values
axis_contrast_curvse.plot(
separations_arcsec,
tmp_flux_ratios,
color = colors[i],
label=num_components)
axis_contrast_curvse.fill_between(
separations_arcsec,
tmp_flux_ratios + tmp_errors,
tmp_flux_ratios - tmp_errors,
color = colors[i],
alpha=0.5)
i+=1
axis_contrast_curvse.set_yscale("log")
# ------------ Plot the overall best -------------------------
axis_contrast_curvse.plot(
separations_arcsec,
overall_best,
color = colors[i],
lw=3,
ls="--",
label="Best")
# ------------- Double axis and limits -----------------------
lim_mag_y = (12.5, 6)
lim_arcsec_x = (0.1, 1.3)
sep_lambda_arcse = interpolate.interp1d(
separations_arcsec,
separations_FWHM,
fill_value='extrapolate')
axis_contrast_curvse_mag = axis_contrast_curvse.twinx()
axis_contrast_curvse_mag.plot(
separations_arcsec,
flux_ratio2mag(tmp_flux_ratios),
alpha=0.)
axis_contrast_curvse_mag.invert_yaxis()
axis_contrast_curvse_lambda = axis_contrast_curvse.twiny()
axis_contrast_curvse_lambda.plot(
separations_FWHM,
tmp_flux_ratios,
alpha=0.)
axis_contrast_curvse.grid(which='both')
axis_contrast_curvse_mag.set_ylim(*lim_mag_y)
axis_contrast_curvse.set_ylim(
mag2flux_ratio(lim_mag_y[0]),
mag2flux_ratio(lim_mag_y[1]))
axis_contrast_curvse.set_xlim(
*lim_arcsec_x)
axis_contrast_curvse_mag.set_xlim(
*lim_arcsec_x)
axis_contrast_curvse_lambda.set_xlim(
*sep_lambda_arcse(lim_arcsec_x))
# ----------- Labels and fontsizes --------------------------
axis_contrast_curvse.set_xlabel(
r"Separation [arcsec]", size=16)
axis_contrast_curvse_lambda.set_xlabel(
r"Separation [FWHM]", size=16)
axis_contrast_curvse.set_ylabel(
r"Planet-to-star flux ratio", size=16)
axis_contrast_curvse_mag.set_ylabel(
r"$\Delta$ Magnitude", size=16)
axis_contrast_curvse.tick_params(
axis='both', which='major', labelsize=14)
axis_contrast_curvse_lambda.tick_params(
axis='both', which='major', labelsize=14)
axis_contrast_curvse_mag.tick_params(
axis='both', which='major', labelsize=14)
axis_contrast_curvse_mag.set_title(
r"$5 \sigma_{\mathcal{N}}$ Contrast Curves",
fontsize=18, fontweight="bold", y=1.1)
# --------------------------- Legend -----------------------
handles, labels = axis_contrast_curvse.\
get_legend_handles_labels()
leg1 = fig.legend(handles, labels,
bbox_to_anchor=(0.12, -0.08),
fontsize=14,
title="# PCA components",
loc='lower left', ncol=8)
_=plt.setp(leg1.get_title(),fontsize=14)
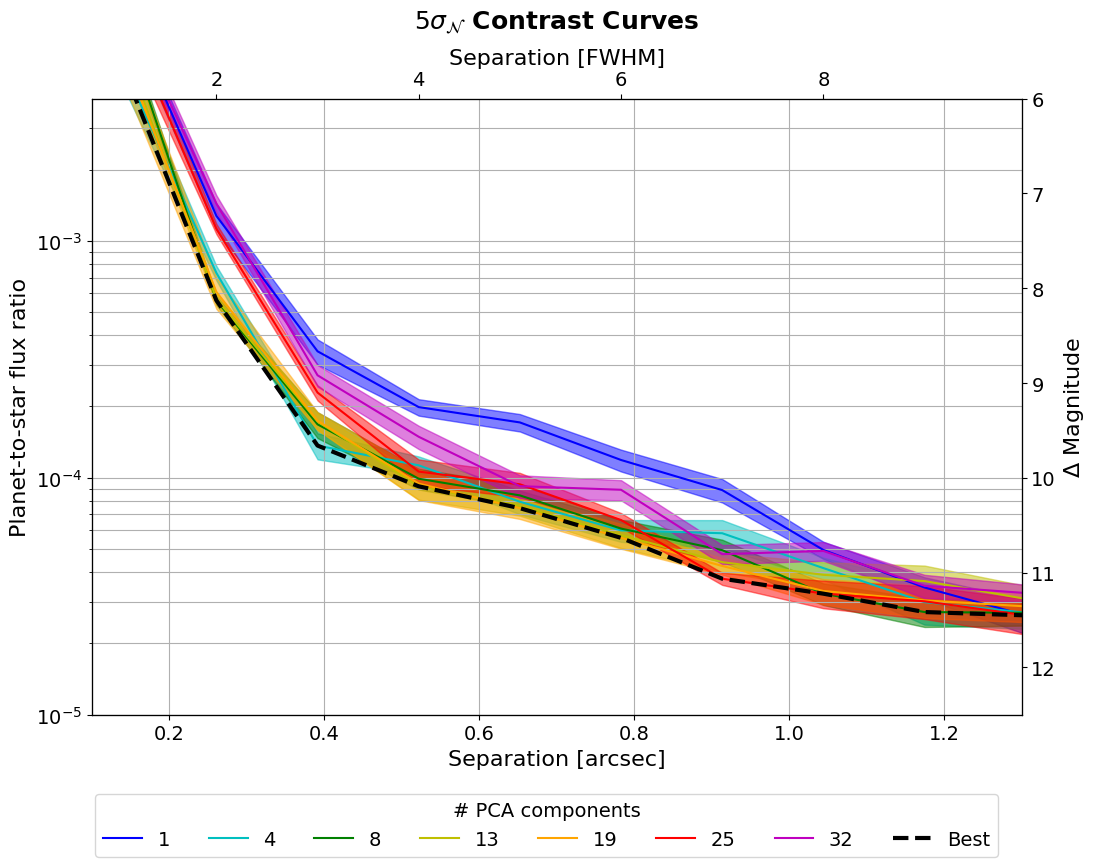
Now let’s plot the optimal number of principal components as a function of separation:
[61]:
if applefy_installed:
plt.figure(figsize=(12, 8))
plt.plot(separations_arcsec,
np.array(components)[np.argmin(
contrast_curves.values,
axis=1)],)
plt.title(r"Best number of PCA components",
fontsize=18, fontweight="bold", y=1.1)
plt.tick_params(axis='both', which='major', labelsize=14)
plt.xlabel("Separation [arcsec]", fontsize=16)
plt.ylabel("Number of PCA components", fontsize=16)
plt.grid()
ax2 = plt.twiny()
ax2.plot(separations_FWHM,
np.array(components)[
np.argmin(contrast_curves.values, axis=1)],)
ax2.set_xlabel("Separation [FWHM]", fontsize=16)
ax2.tick_params(axis='both', which='major', labelsize=14)
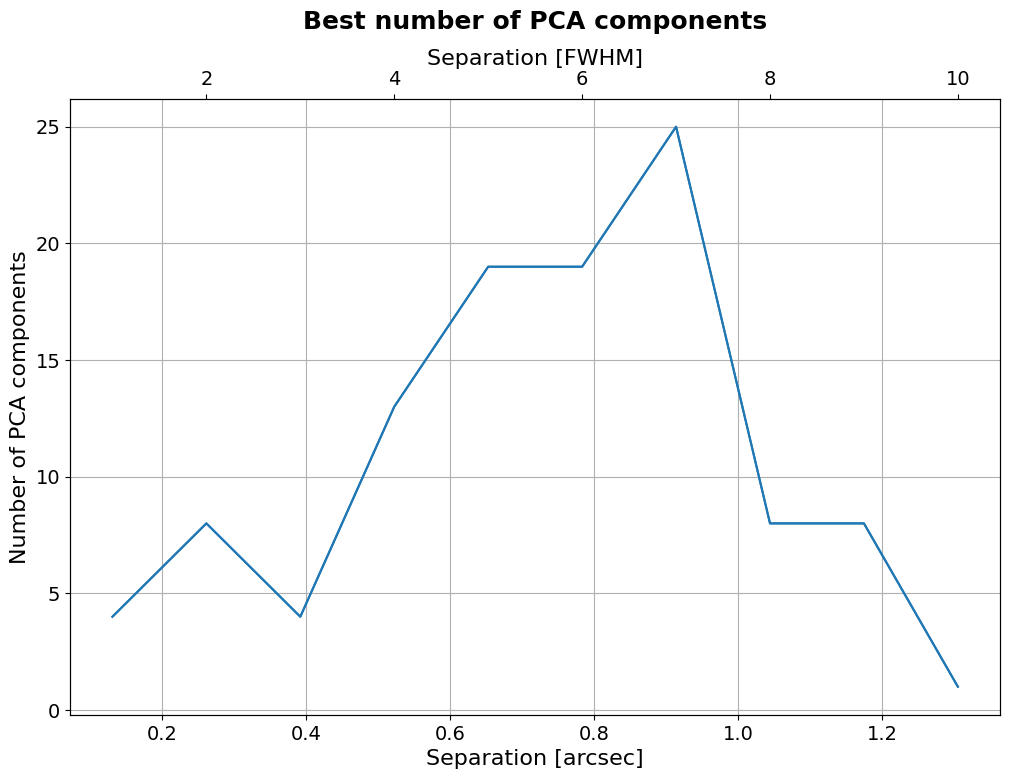
4.6.2. Applefy contrast grids
Again, let’s start by defining a contrast instance, along with a checkpoint directory:
[62]:
checkpoint_dir = "../datasets/TMP/cg/"
[63]:
if applefy_installed:
if not os.path.isdir(checkpoint_dir):
os.makedirs(checkpoint_dir)
contrast_instance = Contrast(science_sequence=cube_emp, psf_template=psfn, parang_rad=angs,
psf_fwhm_radius=fwhm_naco/2, dit_psf_template=1., dit_science=starphot,
scaling_factor=1., # A factor to account e.g. for ND filters
checkpoint_dir=checkpoint_dir)
Let’s define the brightness and number of fake planets to be injected - this time we’ll consider a range in contrasts:
[64]:
flux_ratios_mag = np.linspace(7.5, 12, 10) # magnitude differences of injected fake planets
num_fake_planets = 3 # number of injected fake planets azimuthally
[65]:
if applefy_installed:
from applefy.utils import flux_ratio2mag, mag2flux_ratio
flux_ratios = mag2flux_ratio(flux_ratios_mag)
print("{} fake planets will be injected azimuthally at {} flux ratios ({} mag difference)".format(num_fake_planets,
flux_ratios,
flux_ratios_mag))
3 fake planets will be injected azimuthally at [1.00000000e-03 6.30957344e-04 3.98107171e-04 2.51188643e-04
1.58489319e-04 1.00000000e-04 6.30957344e-05 3.98107171e-05
2.51188643e-05 1.58489319e-05] flux ratios ([ 7.5 8. 8.5 9. 9.5 10. 10.5 11. 11.5 12. ] mag difference)
[66]:
if applefy_installed:
contrast_instance.design_fake_planet_experiments(flux_ratios=flux_ratios,
num_planets=num_fake_planets,
overwrite=True)
Overwriting existing config files.
Let’s now run the fake planet experiment. For this we consider a grid of tested numbers of principal components:
[67]:
if applefy_installed:
from applefy.wrappers.vip import MultiComponentPCAvip
algorithm_function = MultiComponentPCAvip(num_pcas=components, kwarg={'verbose':False})
contrast_instance.run_fake_planet_experiments(algorithm_function=algorithm_function,
num_parallel=cpu_count()//2)
Running fake planet experiments...
100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 301/301 [15:00<00:00, 2.99s/it]
[DONE]
Select the aperture photometry mode (choice between spaced pixels “FS” or aperture sums “ASS”):
[68]:
if applefy_installed:
from applefy.utils.photometry import AperturePhotometryMode
# Use apertures pixel values
photometry_mode_planet = AperturePhotometryMode(
"ASS", # or "AS"
psf_fwhm_radius=fwhm_naco/2,
search_area=0.5)
photometry_mode_noise = AperturePhotometryMode(
"AS",
psf_fwhm_radius=fwhm_naco/2)
[69]:
if applefy_installed:
contrast_instance.prepare_contrast_results(
photometry_mode_planet=photometry_mode_planet,
photometry_mode_noise=photometry_mode_noise)
Select the statistical test to be used:
[70]:
if applefy_installed:
from applefy.statistics import TTest, gaussian_sigma_2_fpf, fpf_2_gaussian_sigma, LaplaceBootstrapTest
[71]:
if applefy_installed:
statistical_test = TTest()
Let’s then calculate the contrast grids (i.e. the FPF expressed in Gaussian \(\sigma\) for different numbers of principal components and different injected contrasts; see all options in the Applefy tutorial)
[72]:
if applefy_installed:
contrast_curves_grid, contrast_grids = contrast_instance.compute_contrast_grids(
statistical_test=statistical_test,
num_cores=cpu_count()//2,
confidence_level_fpf=gaussian_sigma_2_fpf(5),
num_rot_iter=20,
safety_margin=1.0,
pixel_scale=pxscale_naco)
Computing contrast grid for PCA (001 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Computing contrast grid for PCA (004 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Computing contrast grid for PCA (008 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Computing contrast grid for PCA (013 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Computing contrast grid for PCA (019 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Computing contrast grid for PCA (025 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Computing contrast grid for PCA (032 components)
Computing contrast grid with multiprocessing:
....................................................................................................[DONE]
Two outputs are obtained: contrast grids (in the form of a dictionary, one grid for each number of PCs) and contrast curves obtained by thresholding the contrast grids (in the form of a Pandas table).
4.6.2.1. Visualizing the contrast grids
[73]:
if applefy_installed:
print(contrast_curves_grid)
PCA (001 components) \
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 inf
3.0 0.391611 0.000317
4.0 0.522148 0.000205
5.0 0.652685 0.000160
6.0 0.783222 0.000112
7.0 0.913759 0.000086
8.0 1.044296 0.000050
9.0 1.174833 0.000031
10.0 1.305370 0.000025
PCA (004 components) \
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 0.000757
3.0 0.391611 0.000167
4.0 0.522148 0.000115
5.0 0.652685 0.000085
6.0 0.783222 0.000060
7.0 0.913759 0.000051
8.0 1.044296 0.000044
9.0 1.174833 0.000026
10.0 1.305370 0.000027
PCA (008 components) \
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 0.000611
3.0 0.391611 0.000161
4.0 0.522148 0.000103
5.0 0.652685 0.000093
6.0 0.783222 0.000061
7.0 0.913759 0.000047
8.0 1.044296 0.000034
9.0 1.174833 0.000023
10.0 1.305370 0.000026
PCA (013 components) \
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 0.000524
3.0 0.391611 0.000148
4.0 0.522148 0.000086
5.0 0.652685 0.000074
6.0 0.783222 0.000052
7.0 0.913759 0.000041
8.0 1.044296 0.000040
9.0 1.174833 0.000037
10.0 1.305370 0.000030
PCA (019 components) \
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 0.000565
3.0 0.391611 0.000120
4.0 0.522148 0.000070
5.0 0.652685 0.000067
6.0 0.783222 0.000049
7.0 0.913759 0.000038
8.0 1.044296 0.000035
9.0 1.174833 0.000026
10.0 1.305370 0.000029
PCA (025 components) \
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 0.000954
3.0 0.391611 0.000108
4.0 0.522148 0.000056
5.0 0.652685 0.000063
6.0 0.783222 0.000047
7.0 0.913759 0.000030
8.0 1.044296 0.000027
9.0 1.174833 0.000021
10.0 1.305370 0.000022
PCA (032 components)
separation [$FWHM$] separation [arcsec]
1.0 0.130537 inf
2.0 0.261074 inf
3.0 0.391611 0.000113
4.0 0.522148 0.000061
5.0 0.652685 0.000048
6.0 0.783222 0.000049
7.0 0.913759 0.000033
8.0 1.044296 0.000032
9.0 1.174833 0.000023
10.0 1.305370 0.000023
Let’s check the results for 19 principal components:
[76]:
ex_pc = 19
[77]:
if applefy_installed:
example_grid = contrast_grids["PCA ({:03d} components)".format(ex_pc)]
# convert FPF to Gaussian Sigma
example_grid = example_grid.map(fpf_2_gaussian_sigma)
# convert flux_ratio to mag
example_grid.index = flux_ratio2mag(example_grid.index)
print(example_grid)
separation [FWHM] 1.0 2.0 3.0 4.0 5.0 \
flux_ratio
7.5 2.008370 5.394783 7.666906 9.483116 10.824543
8.0 2.062938 5.114021 7.368064 9.142008 10.514931
8.5 1.941543 4.635351 7.089383 8.675803 9.914510
9.0 1.877863 3.933987 6.378800 7.970985 8.895517
9.5 1.696185 3.065047 5.516982 7.075826 7.736946
10.0 1.305535 2.459888 4.664974 5.892618 6.279798
10.5 1.006822 1.969059 3.814828 4.732727 4.793840
11.0 0.835541 1.583005 3.104087 3.614169 3.347586
11.5 0.715274 1.312736 2.550214 2.695277 2.247183
12.0 0.644244 1.137645 2.142353 2.001203 1.440163
separation [FWHM] 6.0 7.0 8.0 9.0 10.0
flux_ratio
7.5 11.656312 12.590658 13.544075 14.641647 15.542328
8.0 11.256106 12.057257 13.028396 14.184473 15.096176
8.5 10.735447 11.499449 12.528246 13.502048 14.495459
9.0 9.881211 10.786152 11.771061 12.671839 13.661081
9.5 8.760552 9.767830 10.583830 11.624414 12.414664
10.0 7.313060 8.310939 9.226578 10.156350 10.616768
10.5 5.818723 6.785923 7.532526 8.282083 8.496921
11.0 4.325298 5.134021 5.488361 6.555087 6.320718
11.5 3.143441 3.624079 3.720914 4.880726 4.480109
12.0 2.208254 2.491451 2.312835 3.502819 3.011140
Quick Note: The plotting code below relies on seaborn, which is not a mandatory dependence of VIP. If you wish to plot the contrast grid result in a nice way, as below, you will need to pip install seaborn.
[78]:
def plot_contrast_grid(
contrast_grid_axis,
colorbar_axis,
contrast_grid):
c_bar_kargs = dict(
orientation = "vertical",
label = r"Confidence [$\sigma_{\mathcal{N}}$]")
heat = sns.heatmap(
contrast_grid,
vmax=2, vmin=7,
annot=True,
cmap="YlGnBu",
ax=contrast_grid_axis,
cbar_ax=colorbar_axis,
cbar_kws=c_bar_kargs)
ylabels = ['{:.1f}'.format(float(x.get_text()))
for x in heat.get_yticklabels()]
_=heat.set_yticklabels(ylabels)
xlabels = ['{:.1f}'.format(float(x.get_text()))
for x in heat.get_xticklabels()]
_=heat.set_xticklabels(xlabels)
[79]:
if applefy_installed:
if not no_sns:
fig = plt.figure(figsize=(8, 4))
gs0 = fig.add_gridspec(1, 1)
gs0.update(wspace=0.0, hspace=0.2)
gs1 = gridspec.GridSpecFromSubplotSpec(
1, 2, subplot_spec = gs0[0],
wspace=0.05, width_ratios=[1, 0.03])
# All axis we need
contrast_ax = fig.add_subplot(gs1[0])
colorbar_ax = fig.add_subplot(gs1[1])
# Plot the contrast grid
plot_contrast_grid(
contrast_grid_axis=contrast_ax,
colorbar_axis=colorbar_ax,
contrast_grid=example_grid)
colorbar_ax.yaxis.label.set_size(14)
contrast_ax.set_ylabel(
"Contrast - $c = f_p / f_*$ - [mag]", size=14)
contrast_ax.set_xlabel(
r"Separation [FWHM]", size=14)
contrast_ax.set_title(
"Contrast Grid with {} PCA components".format(ex_pc),
fontsize=16,
fontweight="bold",
y=1.03)
contrast_ax.tick_params(
axis='both',
which='major',
labelsize=12)
# Save the figure
fig.patch.set_facecolor('white')
else:
print("To be able to plot the contrast grid results, you will need seaborn installed (e.g. pip install seaborn).")
To be able to plot the contrast grid results, you will need seaborn installed (e.g. pip install seaborn).
4.6.2.2. Visualizing the thresholded contrast curves
[80]:
if applefy_installed:
# compute the overall best contrast curve
overall_best = np.min(contrast_curves_grid.values, axis=1)
[81]:
# Find one color for each number of PCA components used.
if applefy_installed:
if no_sns:
colors = ['b','c','g','y','orange','r','m','k']
else:
# nicer plotting if seaborn installed
colors = sns.color_palette("rocket_r",
n_colors=len(contrast_curves.columns))
colors
[82]:
if applefy_installed:
separations_arcsec = contrast_curves_grid.reset_index(level=0).index
separations_FWHM = contrast_curves_grid.reset_index(level=1).index
[83]:
if applefy_installed:
# 1.) Create Plot Layout
fig = plt.figure(constrained_layout=False, figsize=(12, 8))
gs0 = fig.add_gridspec(1, 1)
axis_contrast_curvse = fig.add_subplot(gs0[0, 0])
# ---------------------- Create the Plot --------------------
i = 0 # color picker
for tmp_model in contrast_curves_grid.columns:
num_components = int(tmp_model[6:9])
tmp_flux_ratios = contrast_curves_grid.reset_index(
level=0)[tmp_model].values
axis_contrast_curvse.plot(separations_arcsec,
tmp_flux_ratios,
color = colors[i],
label=num_components)
i+=1
axis_contrast_curvse.set_yscale("log")
# ------------ Plot the overall best -------------------------
axis_contrast_curvse.plot(
separations_arcsec,
overall_best,
color = colors[-1],
lw=3,
ls="--",
label="Best")
# ------------- Double axis and limits -----------------------
lim_mag_y = (12.5, 8)
lim_arcsec_x = (0.15, 1.3)
sep_lambda_arcse = interpolate.interp1d(
separations_arcsec,
separations_FWHM,
fill_value='extrapolate')
axis_contrast_curvse_mag = axis_contrast_curvse.twinx()
axis_contrast_curvse_mag.plot(
separations_arcsec,
flux_ratio2mag(tmp_flux_ratios),
alpha=0.)
axis_contrast_curvse_mag.invert_yaxis()
axis_contrast_curvse_lambda = axis_contrast_curvse.twiny()
axis_contrast_curvse_lambda.plot(
separations_FWHM,
tmp_flux_ratios,
alpha=0.)
axis_contrast_curvse.grid(which='both')
axis_contrast_curvse_mag.set_ylim(*lim_mag_y)
axis_contrast_curvse.set_ylim(
mag2flux_ratio(lim_mag_y[0]),
mag2flux_ratio(lim_mag_y[1]))
axis_contrast_curvse.set_xlim(
*lim_arcsec_x)
axis_contrast_curvse_mag.set_xlim(
*lim_arcsec_x)
axis_contrast_curvse_lambda.set_xlim(
*sep_lambda_arcse(lim_arcsec_x))
# ----------- Labels and fontsizes --------------------------
axis_contrast_curvse.set_xlabel(
r"Separation [arcsec]", size=16)
axis_contrast_curvse_lambda.set_xlabel(
r"Separation [FWHM]", size=16)
axis_contrast_curvse.set_ylabel(
r"Planet-to-star flux ratio", size=16)
axis_contrast_curvse_mag.set_ylabel(
r"$\Delta$ Magnitude", size=16)
axis_contrast_curvse.tick_params(
axis='both', which='major', labelsize=14)
axis_contrast_curvse_lambda.tick_params(
axis='both', which='major', labelsize=14)
axis_contrast_curvse_mag.tick_params(
axis='both', which='major', labelsize=14)
axis_contrast_curvse_mag.set_title(
r"$5 \sigma_{\mathcal{N}}$ Contrast Curves",
fontsize=18, fontweight="bold", y=1.1)
# --------------------------- Legend -----------------------
handles, labels = axis_contrast_curvse.\
get_legend_handles_labels()
leg1 = fig.legend(handles, labels,
bbox_to_anchor=(0.22, -0.08),
fontsize=14,
title="# PCA components",
loc='lower left', ncol=8)
_=plt.setp(leg1.get_title(),fontsize=14)
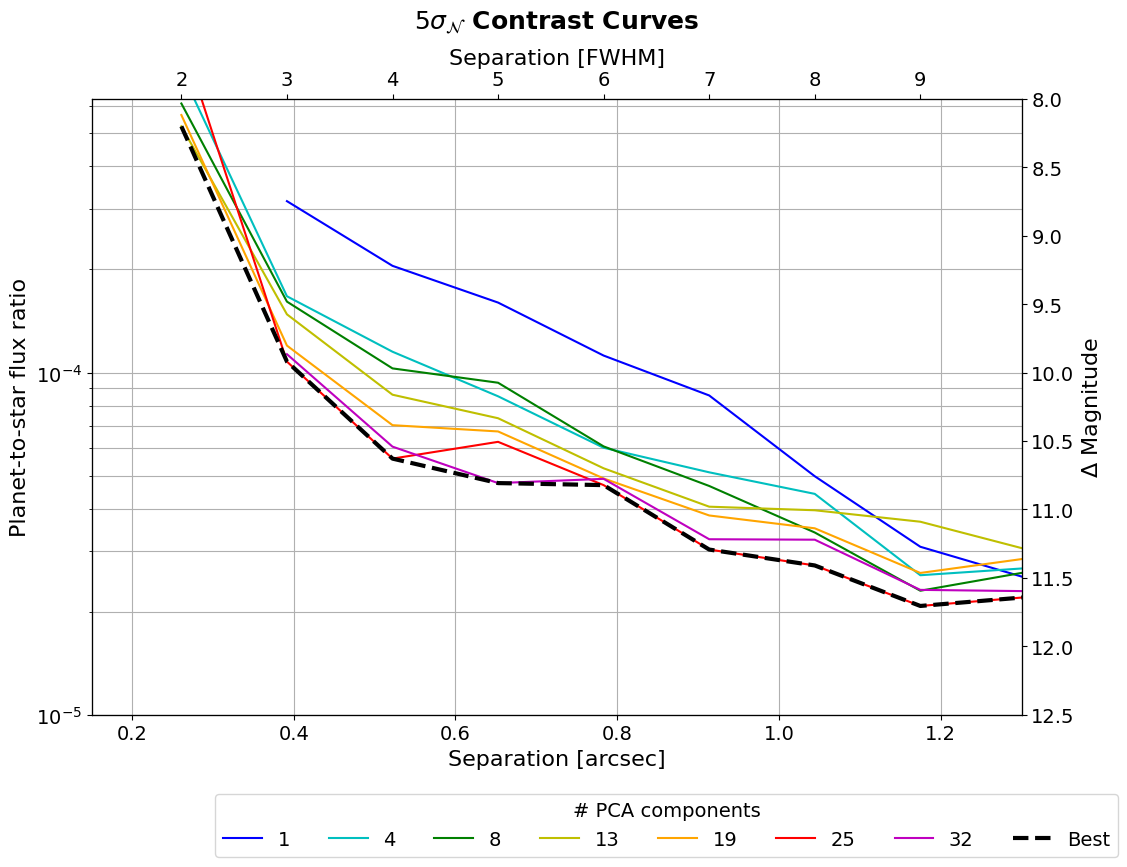
As can be seen, the number of PCs has a clear effect on the achieved contrast.
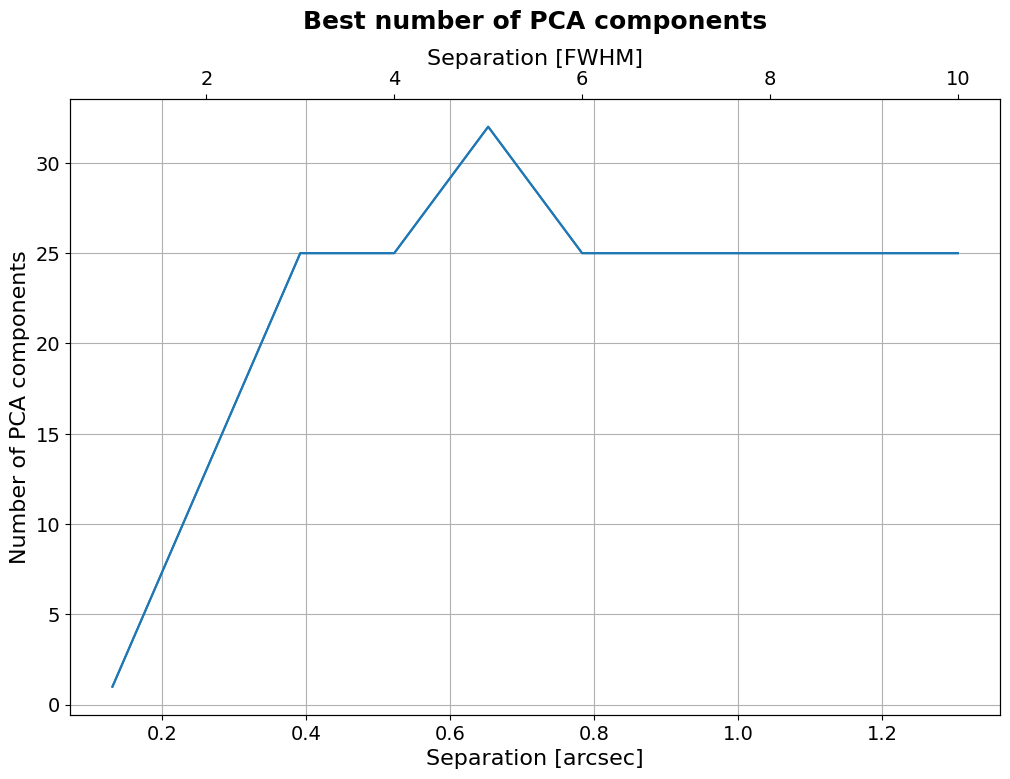
Let’s finally determine the optimal number of principal components as a function of separation. For that, let’s first explicitly define components:
[84]:
if applefy_installed:
plt.figure(figsize=(12, 8))
plt.plot(separations_arcsec,
np.array(components)[np.argmin(
contrast_curves_grid.values,
axis=1)],)
plt.title(r"Best number of PCA components",
fontsize=18, fontweight="bold", y=1.1)
plt.tick_params(axis='both', which='major', labelsize=14)
plt.xlabel("Separation [arcsec]", fontsize=16)
plt.ylabel("Number of PCA components", fontsize=16)
plt.grid()
ax2 = plt.twiny()
ax2.plot(separations_FWHM,
np.array(components)[
np.argmin(contrast_curves_grid.values, axis=1)],)
ax2.set_xlabel("Separation [FWHM]", fontsize=16)
ax2.tick_params(axis='both', which='major', labelsize=14)