5A. ADI forward modeling of point sources
Authors: Valentin Christiaens and Carlos Alberto Gomez GonzalezSuitable for VIP v1.0.3 onwardsLast update: 2024/03/25
Table of contents
This tutorial shows:
how to generate and inject fake companions in a cube;
how to estimate the astrometry and photometry of a directly imaged companion, and associated uncertainties.
Let’s first import a couple of external packages needed in this tutorial:
[1]:
%matplotlib inline
from hciplot import plot_frames, plot_cubes
from matplotlib.pyplot import *
from matplotlib import pyplot as plt
import numpy as np
from packaging import version
In the following box we check that your version of VIP passes the requirements to run this notebook:
[2]:
import vip_hci as vip
vvip = vip.__version__
print("VIP version: ", vvip)
if version.parse(vvip) <= version.parse("1.0.3"):
msg = "Please upgrade your version of VIP"
msg+= "It should be strictly above 1.0.3 to run this notebook."
raise ValueError(msg)
VIP version: 1.6.0
5.1. Loading ADI data
In the ‘dataset’ folder of the VIP_extras repository you can find a toy ADI (Angular Differential Imaging) cube and a NACO point spread function (PSF) to demonstrate the capabilities of VIP. This is an L’-band VLT/NACO dataset of beta Pictoris published in Absil et al. (2013) obtained using the Annular Groove Phase Mask (AGPM) Vortex coronagraph. The sequence has been heavily sub-sampled temporarily to make it
smaller. The frames were also cropped to the central 101x101 area. In case you want to plug-in your cube just change the path of the following cells.
More info on this dataset, and on opening and visualizing fits files with VIP in general, is available in Tutorial 1. Quick start.
Let’s load the data:
[3]:
from vip_hci.fits import open_fits
psfnaco = '../datasets/naco_betapic_psf.fits'
cubename = '../datasets/naco_betapic_cube_cen.fits'
angname = '../datasets/naco_betapic_pa.fits'
cube = open_fits(cubename)
psf = open_fits(psfnaco)
angs = open_fits(angname)
FITS HDU-0 data successfully loaded. Data shape: (61, 101, 101)
FITS HDU-0 data successfully loaded. Data shape: (39, 39)
FITS HDU-0 data successfully loaded. Data shape: (61,)
Let’s fit the PSF with a 2D Gaussian to infer the FWHM, the flux in a 1-FWHM size aperture, and get a flux-normalized PSF:
[4]:
%matplotlib inline
from vip_hci.fm import normalize_psf
psfn, flux, fwhm_naco = normalize_psf(psf, size=19, debug=True, full_output=True)
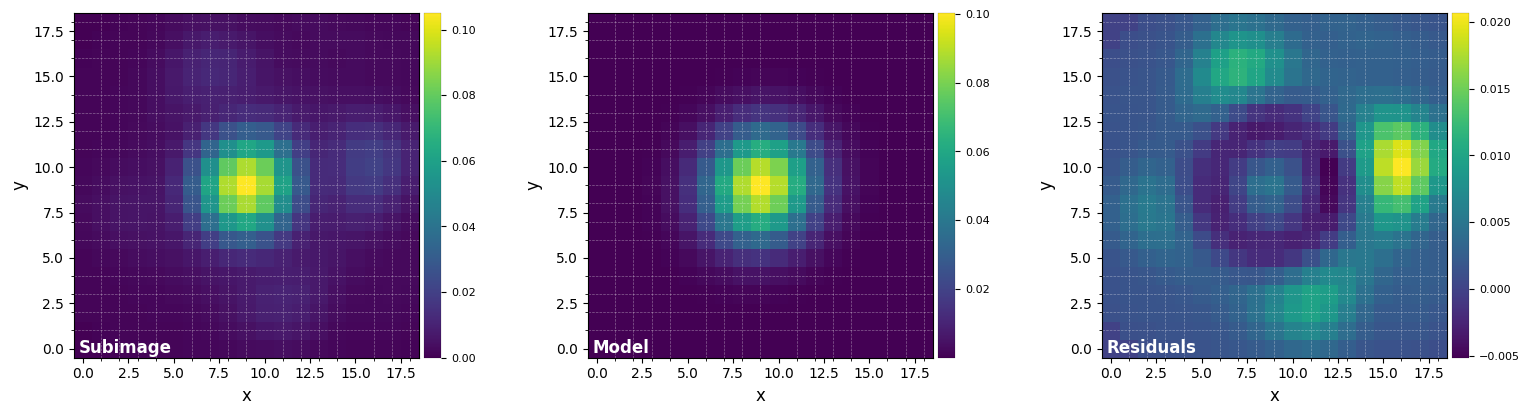
FWHM_y = 4.926059872957138
FWHM_x = 4.675778895005929
centroid y = 9.010992107833063
centroid x = 9.01917912265807
centroid y subim = 9.010992107833063
centroid x subim = 9.01917912265807
amplitude = 0.10032285220380603
theta = -38.446187060503874
Mean FWHM: 4.801
Flux in 1xFWHM aperture: 1.307
[5]:
print(fwhm_naco)
4.800919383981533
Let’s visualize the flux-normalized PSF:
[6]:
plot_frames(psfn, grid=True, size_factor=4)
Let’s finally define the pixel scale for NACO (L’ band), which we get from a dictionary stored in the config subpackage:
[7]:
from vip_hci.config import VLT_NACO
pxscale_naco = VLT_NACO['plsc']
print(pxscale_naco, "arcsec/px")
0.02719 arcsec/px
5.2. Generating and injecting synthetic planets
We first select an image library imlib for image operations (shifts, rotations) and associated interpolation order. ‘vip-fft’ is more accurate, but ‘skimage’ is faster, and ‘opencv’ even faster - see Tutorial 7 for more details.
[8]:
imlib_rot = 'skimage' # If you have opencv installed, feel free to set this parameter to" 'opencv'
interpolation= 'biquintic' # If you have opencv installed, feel free to set this parameter to 'lanczos4'
The cube_inject_companions function in the fm module (VIP versions >= 1.1.0) makes the injection of fake companions at arbitrary fluxes and locations very easy. The normalized non-coronagraphic PSF should be provided for the injection. If the user does not have access to an observed PSF, the create_synth_psf from the var module can be used to create synthetic ones (based on 2D Gaussian, Moffat or Airy models).
Some procedures, e.g. the negative fake companion technique and the contrast curve generation, heavily rely on the injection of fake companions. The coordinates for the injection should be provided in the derotated image, while the actual injection occurs in the images of the input cube, i.e. in the rotated field.
[9]:
rad_fc = 30.5
theta_fc = 240
flux_fc = 400.
gt = [rad_fc, theta_fc, flux_fc]
[10]:
from vip_hci.fm import cube_inject_companions
cubefc = cube_inject_companions(cube, psf_template=psfn, angle_list=angs, flevel=flux_fc, plsc=pxscale_naco,
rad_dists=[rad_fc], theta=theta_fc, n_branches=1,
imlib=imlib_rot, interpolation=interpolation)
Let’s set the corresponding cartesian coordinates:
[11]:
from vip_hci.var import frame_center
cy, cx = frame_center(cube[0])
x_fc = cx + rad_fc*np.cos(np.deg2rad(theta_fc))
y_fc = cy + rad_fc*np.sin(np.deg2rad(theta_fc))
xy_test = (x_fc, y_fc)
print('({:.1f}, {:.1f})'.format(xy_test[0],xy_test[1]))
(34.7, 23.6)
Let’s double-check the fake companion was injected at the right location, by post-processing the cube and checking the final image. Let’s use PCA, and infer the optimal \(n_{\rm pc}\) while we are at it - this will be useful for the next section.
[12]:
from vip_hci.psfsub import pca_grid
res_ann_opt = pca_grid(cubefc, angs, fwhm=fwhm_naco, range_pcs=(1,41,1), source_xy=xy_test, mode='annular',
annulus_width=4*fwhm_naco, imlib=imlib_rot, interpolation=interpolation,
full_output=True, plot=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-26 01:07:58
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Done SVD/PCA with numpy SVD (LAPACK)
Running time: 0:00:00.013050
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Number of steps 41
Optimal number of PCs = 7, for S/N=11.105
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Coords of chosen px (X,Y) = 34.7, 23.6
Flux in a centered 1xFWHM circular aperture = 146.645
Central pixel S/N = 13.443
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Inside a centered 1xFWHM circular aperture:
Mean S/N (shifting the aperture center) = 11.105
Max S/N (shifting the aperture center) = 15.556
stddev S/N (shifting the aperture center) = 2.665
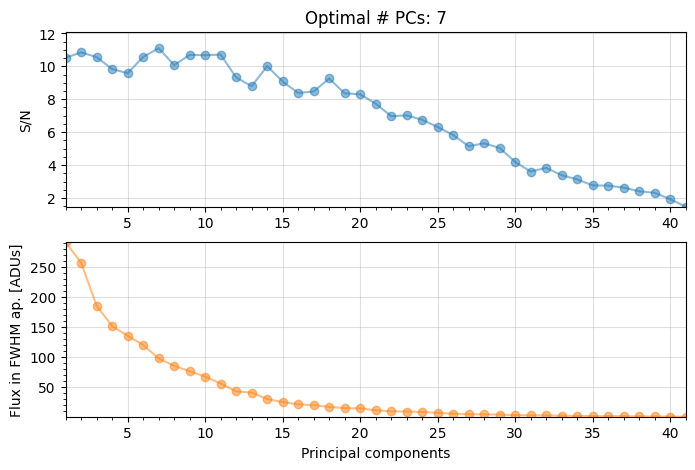
The grid search looking for the optimal number of principal components (npc) found that 10 principal components maximizes the S/N ratio of the injected fake companion.
[13]:
_, final_ann_opt, _, opt_npc_ann = res_ann_opt
[14]:
plot_frames(final_ann_opt, label='PCA-ADI annulus (opt. npc={:.0f})'.format(opt_npc_ann),
dpi=100, vmin=-5, colorbar=True, circle=xy_test)
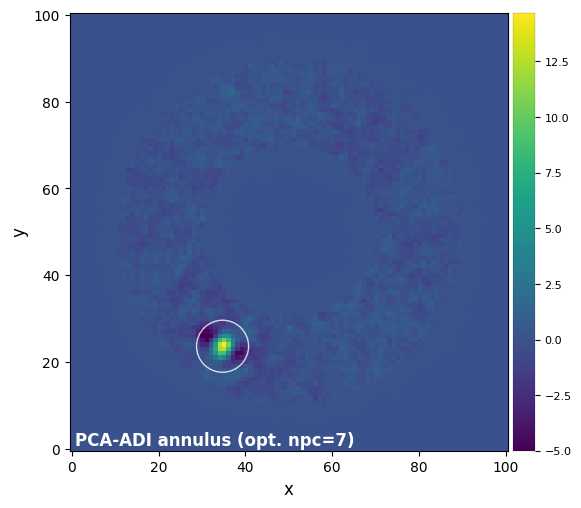
We can see that the fake companion was indeed injected at the requested location.
5.3. Flux and position estimation with NEGFC
When a companion candidate is detected, the next step is to characterize it, i.e. infer its exact position (astrometry) and flux (photometry).
Question 5.1: Why would a simple 2D Gaussian fit (as performed e.g. for the stellar PSF in Section 5.1) be inappropriate to extract the astrometry and photometry of a candidate companion?
VIP implements the Negative fake companion (NEGFC) technique for robust extraction of the position and flux of detected point-like sources. The technique can be summarized as follow (see full description in Wertz et al. 2017):
Estimate the position and flux of the planet, from either the visual inspection of reduced images or a previous estimator (see ABC below).
Scale (in flux) and shift the normalized off-axis PSF to remove the estimate from the input data cube.
Process the cube with PCA in a single annulus encompassing the point source.
Measure residuals in an aperture centered on the approximate location of the companion candidate.
Iterate on the position and flux of the injected negative PSF (steps 2-4), until the absolute residuals in the aperture are minimized (i.e. the injected negative companion flux and the position match exactly that of the true companion).
Iterations between steps 2-4 can be performed in one of 3 ways - sorted in increasing computation time and accuracy:
a grid search on the flux only, provided a fixed estimate of the position (implemented in the
firstguessfunction);a Nelder-Mead simplex algorithm (
firstguessfunction with thesimplex=Trueoption);an MCMC sampler, which has the advantage to also yield uncertainties on each of the parameters of the point source (
mcmc_negfc_samplingfunction).
Different figures of merit can be used for minimization of the residuals (Wertz et al. 2017; Christiaens et al. 2021):
where \(j \in {1,...,N}\), \(N\) is the total number of pixels contained in the circular aperture around the companion candidate, \(\mu\) and \(\sigma\) are the mean and standard deviation (\(N_{\rm resel}\) degrees of freedom) of pixel intensities in a truncated annulus at the radius of the companion candidate, but avoiding the azimuthal region encompassing the negative side lobes.
5.3.1. Nelder-Mead based optimization
With the function firstguess, we can obtain a first estimation of the flux and position by running A) a naive grid minimization (grid of values for the flux through parameter f_range), and B) a Nelder-mead based minimization (if the parameter simplex is set to True). The latter is done based on the preliminary guess of the grid minimization. The maximum number of iterations and error can be set with the parameter simplex_options as a dicitionary (see scipy.minimize function
for the Nelder-Mead options).
Fisrt we define the position of the sources by examining a flux frame or S/N map. planets_xy_coord takes a list or array of X,Y pairs like ((x1,y1),(x2,y2)…(x_n,y_n)). Let’s take the coordinates of the previously injected companion.
Let’s test the algorithm with different values for the # of PCs: 5 and 25.
[15]:
from vip_hci.fm import firstguess
r_lo, theta_lo, f_lo = firstguess(cubefc, angs, psfn, ncomp=5, planets_xy_coord=[xy_test],
fwhm=fwhm_naco, f_range=None, annulus_width=4*fwhm_naco,
aperture_radius=2, simplex=True, imlib=imlib_rot,
interpolation=interpolation, plot=True, verbose=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-26 01:08:04
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Planet 0
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Planet 0: flux estimation at the position [34.749999999999986,23.58622518457463], running ...
Step | flux | chi2r
1/30 0.100 1.619
2/30 0.149 1.618
3/30 0.221 1.618
4/30 0.329 1.617
5/30 0.489 1.616
6/30 0.728 1.614
7/30 1.083 1.612
8/30 1.610 1.608
9/30 2.395 1.602
10/30 3.562 1.594
11/30 5.298 1.582
12/30 7.880 1.563
13/30 11.721 1.536
14/30 17.433 1.495
15/30 25.929 1.436
16/30 38.566 1.352
17/30 57.362 1.233
18/30 85.317 1.053
19/30 126.896 0.817
20/30 188.739 0.521
21/30 280.722 0.216
22/30 417.532 0.061
23/30 621.017 0.545
24/30 923.671 2.828
25/30 1373.824 8.789
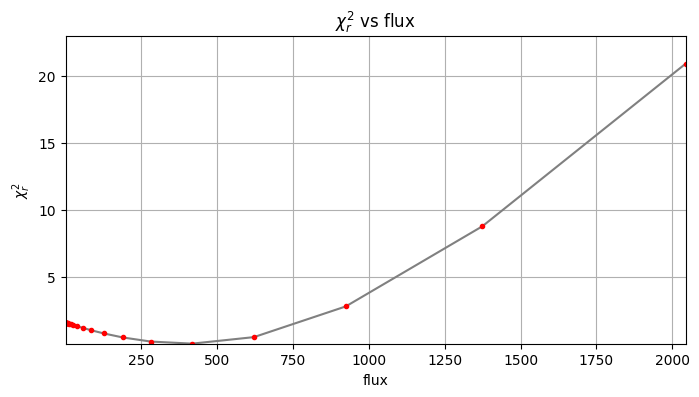
Planet 0: preliminary position guess: (r, theta)=(30.5, 240.0)
Planet 0: preliminary flux guess: 417.5
Planet 0: Simplex Nelder-Mead minimization, running ...
Planet 0: Success: True, nit: 106, nfev: 225, chi2r: 0.055650757580268675
message: Optimization terminated successfully.
Planet 0 simplex result: (r, theta, f)=(30.524, 240.121, 402.627) at
(X,Y)=(34.79, 23.53)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
DONE !
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Running time: 0:00:37.667729
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
[16]:
r_hi, theta_hi, f_hi = firstguess(cubefc, angs, psfn, ncomp=25, planets_xy_coord=[xy_test],
fwhm=fwhm_naco, f_range=None, annulus_width=4*fwhm_naco,
aperture_radius=2, imlib=imlib_rot, interpolation=interpolation,
simplex=True, plot=True, verbose=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-26 01:08:41
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Planet 0
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Planet 0: flux estimation at the position [34.749999999999986,23.58622518457463], running ...
Step | flux | chi2r
1/30 0.100 0.216
2/30 0.149 0.216
3/30 0.221 0.216
4/30 0.329 0.216
5/30 0.489 0.216
6/30 0.728 0.216
7/30 1.083 0.216
8/30 1.610 0.215
9/30 2.395 0.215
10/30 3.562 0.215
11/30 5.298 0.214
12/30 7.880 0.213
13/30 11.721 0.211
14/30 17.433 0.209
15/30 25.929 0.210
16/30 38.566 0.206
17/30 57.362 0.197
18/30 85.317 0.176
19/30 126.896 0.146
20/30 188.739 0.120
21/30 280.722 0.077
22/30 417.532 0.055
23/30 621.017 0.176
24/30 923.671 0.360
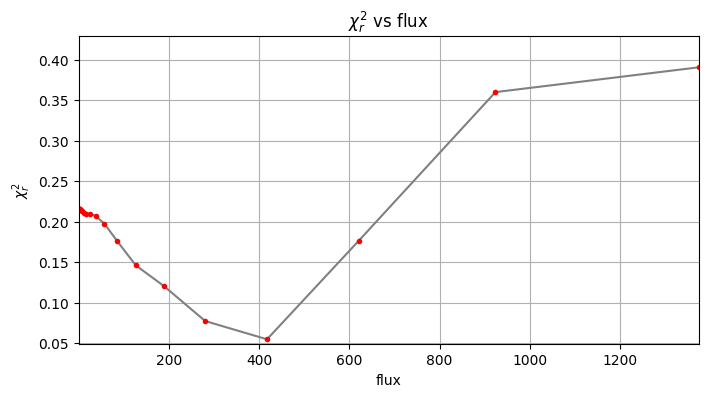
Planet 0: preliminary position guess: (r, theta)=(30.5, 240.0)
Planet 0: preliminary flux guess: 417.5
Planet 0: Simplex Nelder-Mead minimization, running ...
Planet 0: Success: True, nit: 113, nfev: 253, chi2r: 0.050996581021086264
message: Optimization terminated successfully.
Planet 0 simplex result: (r, theta, f)=(30.416, 239.945, 401.511) at
(X,Y)=(34.77, 23.67)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
DONE !
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Running time: 0:00:44.151756
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
For both the \(n_{\rm pc} = 5\) and \(n_{\rm pc} = 25\) cases, the parameters estimated by the Nelder-Mead optimization are not exactly equal to the original values (radius=30.5, theta=240, flux=400), which reflects:
the limitations of this heuristic minization procedure (depending on the initial guess the minimization may get trapped in a different local minimum);
the higher residual speckle noise level in images obtained with low \(n_{\rm pc}\) values;
the higher self-subtraction for high \(n_{\rm pc}\) values.
These estimates are provided without uncertainties (error bars). We will come back to this question later on.
For comparison, let’s use the optimal \(n_{\rm pc} = 10\) found in Section 5.2:
[17]:
r_0, theta_0, f_0 = firstguess(cubefc, angs, psfn, ncomp=opt_npc_ann, planets_xy_coord=[xy_test],
fwhm=fwhm_naco, f_range=None, annulus_width=4*fwhm_naco,
aperture_radius=2, imlib=imlib_rot, interpolation=interpolation,
simplex=True, plot=True, verbose=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-26 01:09:26
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Planet 0
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Planet 0: flux estimation at the position [34.749999999999986,23.58622518457463], running ...
Step | flux | chi2r
1/30 0.100 2.020
2/30 0.149 2.020
3/30 0.221 2.019
4/30 0.329 2.018
5/30 0.489 2.016
6/30 0.728 2.014
7/30 1.083 2.011
8/30 1.610 2.006
9/30 2.395 1.999
10/30 3.562 1.988
11/30 5.298 1.972
12/30 7.880 1.949
13/30 11.721 1.915
14/30 17.433 1.866
15/30 25.929 1.796
16/30 38.566 1.695
17/30 57.362 1.538
18/30 85.317 1.326
19/30 126.896 1.042
20/30 188.739 0.650
21/30 280.722 0.249
22/30 417.532 0.056
23/30 621.017 0.642
24/30 923.671 3.220
25/30 1373.824 10.306
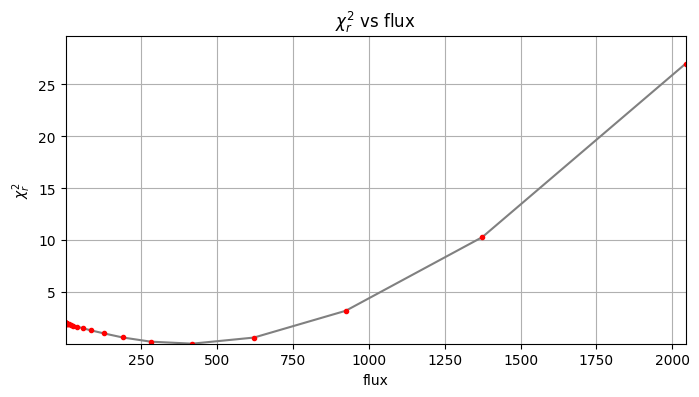
Planet 0: preliminary position guess: (r, theta)=(30.5, 240.0)
Planet 0: preliminary flux guess: 417.5
Planet 0: Simplex Nelder-Mead minimization, running ...
Planet 0: Success: True, nit: 93, nfev: 203, chi2r: 0.05341968802209515
message: Optimization terminated successfully.
Planet 0 simplex result: (r, theta, f)=(30.485, 240.031, 404.544) at
(X,Y)=(34.77, 23.59)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
DONE !
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Running time: 0:00:35.688319
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
We see that using the optimal \(n_{\rm pc}\) leads to closer parameter estimates to the ground truth.
Answer 5.1: If relying on a 2D Gaussian fit, both the photometry and astrometry would be biased by self-subtraction and the negative side lobes.
5.3.2. Planet subtraction
Let’s use the values obtained with the simplex optimization to subtract the planet with the function cube_planet_free.
First we define a list with the parameters (r, theta, flux) is each companion that we obtained via the NegFC, in this case one:
[18]:
plpar_fc = [(r_0[0], theta_0[0], f_0[0])]
[19]:
from vip_hci.fm import cube_planet_free
cube_emp = cube_planet_free(plpar_fc, cubefc, angs, psfn, imlib=imlib_rot, interpolation=interpolation)
Let’s double-check the fake companion was well removed by computing a PCA post-processed image:
[20]:
from vip_hci.psfsub import pca_annulus
fr_pca_emp = pca_annulus(cube_emp, angs, ncomp=opt_npc_ann, annulus_width=4*fwhm_naco,
r_guess=rad_fc, imlib=imlib_rot, interpolation=interpolation)
Let’s take a look at the PSF of the planet in the full-frame PCA final image and the same PSF in the frame resulting of processing the planet-subtracted cube:
[21]:
from vip_hci.preproc import frame_crop
cropped_frame1 = frame_crop(final_ann_opt, cenxy=xy_test, size=15)
New shape: (15, 15)
[22]:
cropped_frame2 = frame_crop(fr_pca_emp, cenxy=xy_test, size=15)
New shape: (15, 15)
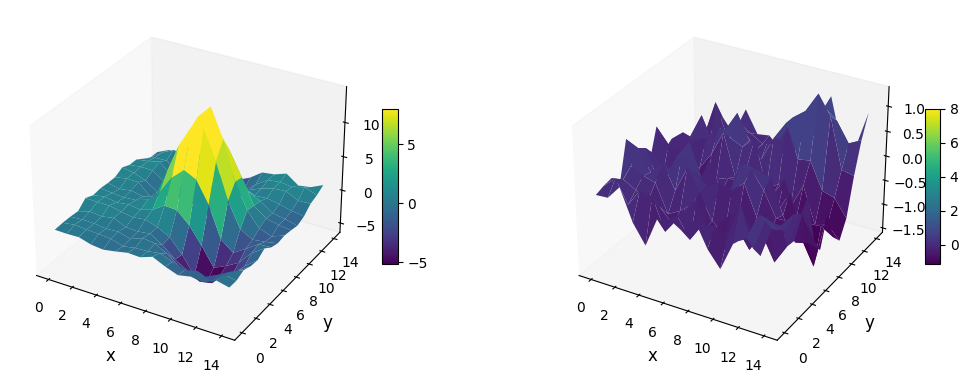
Let’s use both 'mode=surface' and the default image mode of plot_frames to show the residuals in the vicinity of the companion:
[23]:
plot_frames((cropped_frame1, cropped_frame2), mode='surface', vmax=8)
[24]:
plot_frames((final_ann_opt, fr_pca_emp), vmin = float(np.amin(final_ann_opt)),
vmax= float(np.amax(final_ann_opt)), axis=False)
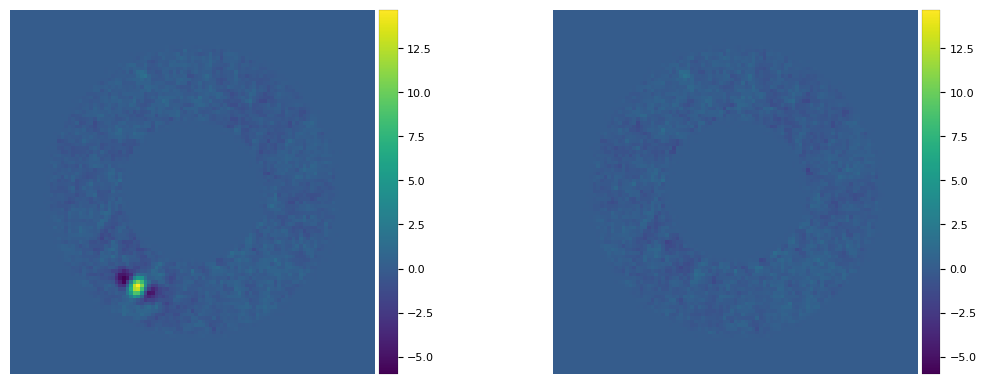
Not only the bright point-like signal is subtracted, but so are the negative side lobes. A subtraction not leaving any significant artifact/defect is a good sign that the inferred parameters are correct. However, keep in mind that even for slightly inaccurate parameters, the final image can still look relatively clean. Let’s take for example the parameters inferred with non-optimal \(n_{\rm pc}\):
[25]:
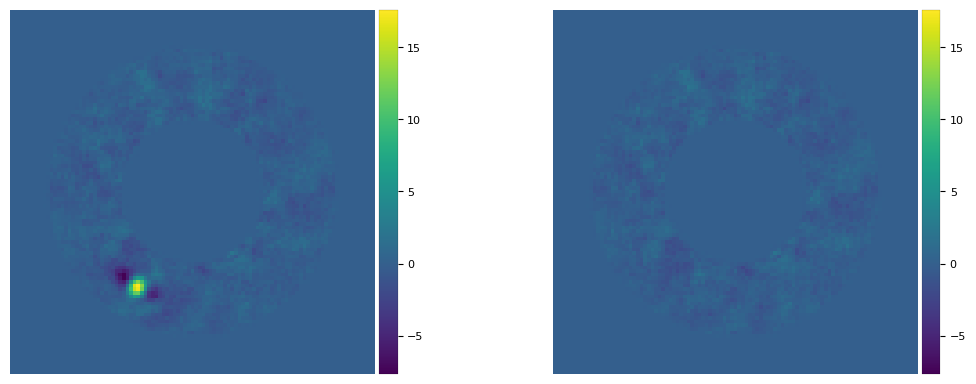
# planet parameters inferred from npc=5 used to make empty cube, then processed with PCA (npc=10)
plpar_fc = [(r_lo[0], theta_lo[0], f_lo[0])]
print(plpar_fc)
cube_emp = cube_planet_free(plpar_fc, cubefc, angs, psfn, imlib=imlib_rot, interpolation=interpolation)
final_ann_5 = pca_annulus(cubefc, angs, ncomp=5, annulus_width=4*fwhm_naco, r_guess=30.5,
imlib=imlib_rot, interpolation=interpolation)
fr_pca_emp5 = pca_annulus(cube_emp, angs, ncomp=5, annulus_width=4*fwhm_naco, r_guess=30.5,
imlib=imlib_rot, interpolation=interpolation)
plot_frames((final_ann_5, fr_pca_emp5), vmin = float(np.amin(final_ann_5)),
vmax= float(np.amax(final_ann_5)), axis=False)
[(30.52433969170673, 240.1209758459184, 402.6266720612793)]
[26]:
# parameters inferred from npc=25 used to make empty cube, then processed with PCA (npc=10)
plpar_fc = [(r_hi[0], theta_hi[0], f_hi[0])]
print(plpar_fc)
cube_emp = cube_planet_free(plpar_fc, cubefc, angs, psfn, imlib=imlib_rot, interpolation=interpolation)
final_ann_25 = pca_annulus(cubefc, angs, ncomp=25, annulus_width=4*fwhm_naco, r_guess=30.5,
imlib=imlib_rot, interpolation=interpolation)
fr_pca_emp25 = pca_annulus(cube_emp, angs, ncomp=25, annulus_width=4*fwhm_naco, r_guess=30.5,
imlib=imlib_rot, interpolation=interpolation)
plot_frames((final_ann_25, fr_pca_emp25), vmin = float(np.amin(final_ann_25)),
vmax= float(np.amax(final_ann_25)), axis=False)
[(30.415536162190293, 239.9454979002353, 401.5113951627229)]
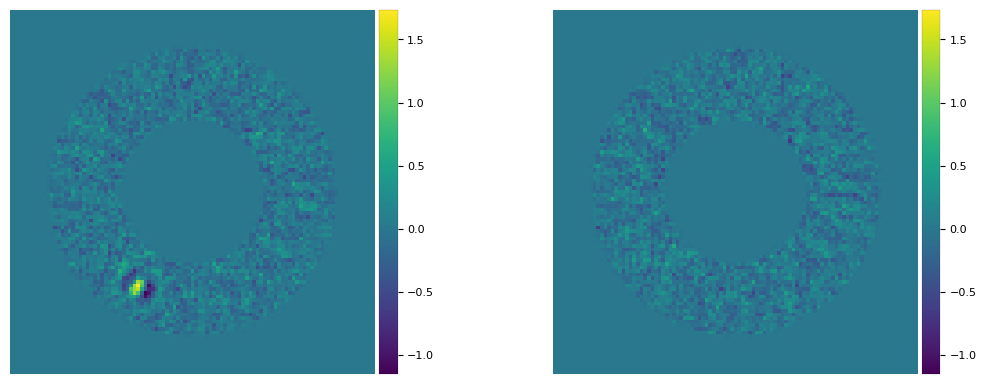
Inaccurate parameters still leading to an apparently good removal of the companion brings the question of the uncertainties on each of the three parameters characterizing the companion. The next sections are dedicated to this question.
5.3.3. NEGFC technique coupled with MCMC
5.3.3.1. Running the MCMC sampler
Markov Chain Monte Carlo (MCMC) is a robust way of obtaining the flux and position of the companion, and their uncertainties. MCMC samples the parameter space (here r and \(\theta\) coordinates, and flux) using a number of walkers following a Markov chain (i.e. a process where each new sampled point only depends on the previous one) for a certain number of iterations. At each iteration, a new sample of parameters is proposed to each walker to explore the parameter space (these are called moves), based on a given proposal function (e.g., the stretch move proposed in Goodman & Weare 2010). A criterion depending on the ratio of likelihoods calculated for the proposed vs the current parameters is then used to accept or reject the proposed moves for the next iteration (if rejected, the parameters do not change).
In our case the log-likelihood is calculated assuming that a perfect subtraction of the companion leads to pixel intensity residuals following a Gaussian distribution (centered on zero, and scaled by the standard deviation estimated in the annulus except in the area of the companion). A convergence criterion based on autocorrelation can be used (and is used by default in VIP) to stop iterating. Sampling the final posterior distributions of the parameters yields both the most likely parameter values and uncertainties on each of them.
The MCMC implementation in VIP leverages `emcee <https://emcee.readthedocs.io/en/stable/>`__ (Foreman-Mackey et al. 2013; check the paper for more details on this implementation of MCMC), which is based on an efficient affine-invariant implementation of MCMC proposed in Goodman & Weare (2010). The relevant function is mcmc_negfc_sampling, which can accept a number of parameters. Let’s define them in the next few boxes:
Let’s first define observation-related parameters, such as the non-coronagraphic psf, its FWHM and the pixel scale od the detector:
[27]:
obs_params = {'psfn': psfn,
'fwhm': fwhm_naco}
In NEGFC, PCA in a single annulus is used by default to speed up the algorithm - although other algorithms can be used through the algo parameter. Let’s set the \(n_{\rm pc}\) to the optimal \(n_{\rm pc}\) found in Section 5.2. We set the width of the annulus on which PCA is performed (in pixels) with the annulus_width parameter. We also set a few other algorithm-related parameters in the following box:
[28]:
annulus_width = 4*fwhm_naco
algo_params = {'algo': pca_annulus,
'ncomp': opt_npc_ann,
'annulus_width': annulus_width,
'svd_mode': 'lapack',
'imlib': imlib_rot,
'interpolation': interpolation}
The choice of log-likelihood expression to be used is determined by mu_sigma and fmerit. If the former is True (default; mu and sigma calculated automatically) or a tuple of 2 values provided manually (corresponding to mean and standard deviation of pixel intensities in an annulus encompassing the companion), the following figure of merit will be used: \(\chi^2 = \sum_j^N \frac{(I_j-\mu)^2}{\sigma^2}\) (as introduced in Christiaens et al.
(2021). Otherwise, the choice will be determined by fmerit: - ‘sum’ for the sum of absolute residuals (details in Wertz et al. 2017); - ‘stddev’ for the standard deviation of residuals (details in Wertz et al. 2017; which can be useful for very faint sources); - ‘hessian’ for the determinant of the local Hessian matrix (which containes 2nd order
derivatives with respect to spatial coordinates) - the latter being useful when the point source is contained within a more extended signal (see e.g. Christiaens et al. 2024).
Another parameter to set is aperture_radius, which is the radius of the aperture (in fwhm units) in which the residual intensities \(I_j\) are considered.
[29]:
mu_sigma=True
aperture_radius=2
negfc_params = {'mu_sigma': mu_sigma,
'aperture_radius': aperture_radius}
Parameter initial_state corresponds to the initial first estimation of the planets parameters (r, theta, flux). We set it to the result of the simplex optimization, obtained with optimal \(n_{\rm pc}\).
[30]:
initial_state = np.array([r_0[0], theta_0[0], f_0[0]])
Beware that the MCMC procedure is a CPU intensive procedure and can take several hours when run properly on a standard laptop. We use the affine invariant sampler from emcee which can be run in parallel (nproc sets the number of CPUs to be used). At least 100 walkers are recommended for our MCMC chain, although both the number of walkers and iterations will depend on your dataset. For the sake of preventing this tutorial to take too long to run, we set the maximum number of iterations to
500, although feel free to significantly increase it in case of non-convergence.
[31]:
from multiprocessing import cpu_count
nwalkers, itermin, itermax = (100, 200, 500)
mcmc_params = {'nwalkers': nwalkers,
'niteration_min': itermin,
'niteration_limit': itermax,
'bounds': None,
'nproc': cpu_count()//2}
Another update from Christiaens et al. (2021) is that the convergence can now be evaluated based on the auto-correlation time (see more details in the documentation of ``emcee` <https://emcee.readthedocs.io/en/stable/tutorials/autocorr/>`__), instead of the Gelman-Rubin test, which is inappropriate for non-independent samples (such as an MCMC chain). We set the convergence test to the autocorrelation time based criterion using conv_test='ac' (instead of Gelman-Rubin ‘gb’). We also set the
autocorrelation criterion \(N/\tau >= a_c\), where \(N\) is the number of samples and \(\tau\) the autocorrelation time, to ac_c=50 (the value recommended in the emcee documentation). Finally, we set the number of consecutive times the criterion must be met to: ac_count_thr=1, and the maximum gap in number of steps between 2 checks of the convergence criterion to: check_maxgap=50. If the maximum number of iterations niteration_limit is large enough, the chain will
stop upon meeting the convergence criterion (spoiler: it won’t be the case here since we chose a small value for niteration_limit).
[32]:
conv_test, ac_c, ac_count_thr, check_maxgap = ('ac', 50, 1, 50)
conv_params = {'conv_test': conv_test,
'ac_c': ac_c,
'ac_count_thr': ac_count_thr,
'check_maxgap': check_maxgap}
Setting bounds=None does not mean no bounds are used for parameter exploration, but rather that they are set automatically to:
\(r \in [r_0-w_{ann}/2, r_0+w_{ann}/2]\), where \(w_{ann}\) is the
annulus_width,\(\theta \in [\theta_0-\Delta {\rm rot}, \theta_0+\Delta {\rm rot}]\), where \(\Delta {\rm rot}\) is the angle subtended by min(
aperture_radius/2,fwhm) at \(r_0\),\(f \in [0.1*f_0, 2*f_0]\),
where (\(r_0, \theta_0, f_0\)) = initial_state. If the bounds are provided manually (as a tuple of tuples), they will supersede the automatic setting above.
Now let’s start the sampler. Note that this step is computer intensive and may take a long time to run depending on your machine. Feel free to skip the next cell if you do not wish to run the MCMC or can’t run it in a reasonable time. The results are already saved as ‘MCMC_results’ in the ‘datasets’ folder and will be loaded in the subsequent boxes.
[33]:
from vip_hci.fm import mcmc_negfc_sampling
chain = mcmc_negfc_sampling(cubefc, angs, **obs_params, **algo_params, **negfc_params,
initial_state=initial_state, **mcmc_params, **conv_params,
display=True, verbosity=2, save=False, output_dir='./')
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-26 00:31:48
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
MCMC sampler for the NEGFC technique
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
The mean and stddev in the annulus at the radius of the companion (excluding the PA area directly adjacent to it) are -0.11 and 1.91 respectively.
Beginning emcee Ensemble sampler...
emcee Ensemble sampler successful
Start of the MCMC run ...
Step | Duration/step (sec) | Remaining Estimated Time (sec)
0 4.67933 2334.98467
1 3.74638 1865.69575
2 3.72469 1851.16845
3 3.69502 1832.72942
4 3.74728 1854.90212
5 3.78942 1871.97447
6 3.83033 1888.35170
7 3.77518 1857.38905
8 3.70591 1819.60034
9 3.75779 1841.31465
10 3.69553 1807.11564
11 3.68184 1796.73743
12 3.70973 1806.64046
13 3.77245 1833.41167
14 3.78166 1834.10656
15 3.75706 1818.41946
16 4.03213 1947.51879
17 3.73734 1801.40029
18 3.69208 1775.89096
19 3.73030 1790.54640
20 3.76877 1805.23987
21 3.68866 1763.17900
22 3.83198 1827.85685
23 3.76373 1791.53358
24 4.08083 1938.39615
25 3.76665 1785.39257
26 3.73637 1767.30301
27 3.66751 1731.06425
28 3.79941 1789.52164
29 3.73613 1755.97969
30 3.73579 1752.08410
31 3.66405 1714.77306
32 3.68651 1721.60064
33 3.65573 1703.57111
34 3.74474 1741.30503
35 3.66804 1701.96824
36 3.66781 1698.19418
37 3.62371 1674.15356
38 3.78592 1745.30912
39 3.65674 1682.09856
40 3.65236 1676.43232
41 3.62254 1659.12149
42 3.64647 1666.43450
43 3.69831 1686.42799
44 3.68725 1677.69784
45 3.77551 1714.08018
46 3.75921 1702.92168
47 3.74600 1693.18974
48 3.71616 1675.98726
49 3.67016 1651.57200
50 3.70370 1662.96040
ac convergence test in progress...
51 3.86112 1729.78131
52 3.66715 1639.21784
53 3.75568 1675.03462
54 3.75262 1669.91679
55 3.69319 1639.77858
56 3.88141 1719.46286
57 3.70450 1637.38812
58 3.67922 1622.53514
59 3.59321 1581.01460
60 3.69739 1623.15245
61 3.69642 1619.03196
62 3.80197 1661.46220
63 3.77312 1645.07901
64 3.79861 1652.39535
65 3.69582 1603.98371
66 3.69055 1598.00772
67 3.66079 1581.45955
68 3.72789 1606.71887
69 3.77428 1622.94212
70 3.68503 1580.87744
71 3.90015 1669.26506
72 3.69125 1576.16546
73 3.72758 1587.94738
74 3.76218 1598.92608
75 3.80940 1615.18772
76 3.78174 1599.67560
77 4.03133 1701.22295
78 4.02550 1694.73634
79 3.73347 1568.05908
80 4.03759 1691.75063
81 3.79961 1588.23865
82 3.84846 1604.80782
83 3.81993 1589.09254
84 3.77626 1567.14790
85 3.93245 1628.03347
86 3.78009 1561.17882
87 3.86868 1593.89575
88 4.11157 1689.85650
89 3.96946 1627.47778
90 3.86380 1580.29297
91 3.81816 1557.80969
92 3.94029 1603.69681
93 3.92043 1591.69580
94 3.98089 1612.26004
95 3.91833 1583.00653
96 3.99442 1609.75086
97 3.85771 1550.79982
98 3.70168 1484.37448
99 3.64839 1459.35760
100 3.62879 1447.88601
ac convergence test in progress...
101 3.93199 1564.93122
102 3.70681 1471.60238
103 3.77023 1493.01068
104 3.67673 1452.30875
105 3.68877 1453.37617
106 3.69146 1450.74535
107 3.68723 1445.39220
108 3.74330 1463.63030
109 3.80973 1485.79665
110 3.77487 1468.42365
111 3.90659 1515.75886
112 3.75022 1451.33591
113 3.73326 1441.03720
114 3.77634 1453.88974
115 3.76211 1444.64870
116 3.73245 1429.52873
117 3.78885 1447.34146
118 3.68469 1403.86689
119 3.76521 1430.77904
120 3.68730 1397.48632
121 3.71669 1404.90995
122 3.65112 1376.47224
123 3.70777 1394.12077
124 3.69306 1384.89563
125 3.71067 1387.78871
126 3.79145 1414.21122
127 3.70668 1378.88608
128 3.69725 1371.68012
129 3.82984 1417.04043
130 3.72761 1375.48772
131 3.67849 1353.68616
132 3.64512 1337.75977
133 3.66435 1341.15210
134 3.87021 1412.62811
135 3.65552 1330.60819
136 3.76853 1367.97675
137 3.71162 1343.60644
138 3.65331 1318.84419
139 3.70705 1334.53728
140 3.70888 1331.48720
141 3.75264 1343.44655
142 3.76311 1343.43063
143 3.85047 1370.76590
144 3.69844 1312.94549
145 3.80945 1348.54530
146 3.72953 1316.52338
147 3.69079 1299.15878
148 3.72498 1307.46728
149 3.68370 1289.29640
150 3.75897 1311.88088
ac convergence test in progress...
151 4.18220 1455.40490
152 3.67940 1276.75284
153 3.65065 1263.12352
154 3.68976 1272.96617
155 3.70908 1275.92524
156 3.76145 1290.17666
157 3.74829 1281.91552
158 3.71551 1266.99061
159 3.70559 1259.90060
160 3.71027 1257.78051
161 3.64383 1231.61589
162 3.81980 1287.27092
163 3.71129 1246.99378
164 3.70950 1242.68350
165 3.70225 1236.55284
166 3.75776 1251.33408
167 3.83048 1271.72036
168 3.65457 1209.66234
169 3.71160 1224.82668
170 3.66088 1204.43116
171 3.71227 1217.62390
172 3.79538 1241.08893
173 3.81336 1243.15503
174 3.90436 1268.91570
175 3.86290 1251.57863
176 3.72057 1201.74508
177 3.67514 1183.39411
178 3.68449 1182.71969
179 3.71312 1188.20000
180 3.71258 1184.31430
181 3.81661 1213.68039
182 3.69779 1172.19975
183 3.69262 1166.86918
184 3.68606 1161.10764
185 3.79154 1190.54450
186 3.71366 1162.37683
187 3.75070 1170.21965
188 3.84512 1195.83325
189 3.76926 1168.47215
190 3.83409 1184.73412
191 3.83113 1179.98712
192 3.72274 1142.88179
193 3.69719 1131.34075
194 3.73633 1139.58035
195 3.70804 1127.24507
196 3.69064 1118.26362
197 3.68163 1111.85286
198 3.68952 1110.54432
199 3.93021 1179.06210
200 3.70211 1106.93059
ac convergence test in progress...
Auto-corr tau/N = [0.0679942 0.07448097 0.06289897]
tau/N <= 0.02 = [False False False]
201 4.11104 1225.08843
202 3.69734 1098.11146
203 3.72829 1103.57502
204 3.84626 1134.64611
205 3.75331 1103.47167
206 3.73777 1095.16690
207 3.79210 1107.29174
208 3.75526 1092.78008
209 3.74581 1086.28635
210 3.70649 1071.17445
211 3.72604 1073.10038
212 3.72992 1070.48589
213 3.67216 1050.23719
214 3.84512 1095.85948
215 3.83460 1089.02725
216 3.72182 1053.27421
217 3.68887 1040.26106
218 3.70251 1040.40503
219 3.80024 1064.06608
220 3.74797 1045.68391
221 3.83778 1066.90256
222 3.73339 1034.14986
223 3.75684 1036.88729
224 3.65747 1005.80453
225 3.66277 1003.59898
226 3.78506 1033.32193
227 3.74414 1018.40526
228 3.70013 1002.73523
229 3.69294 997.09272
230 3.65010 981.87717
231 3.66737 982.85409
232 3.67341 980.80100
233 3.66254 974.23617
234 3.71140 983.52047
235 3.71121 979.75944
236 3.81206 1002.57152
237 3.78130 990.70112
238 3.74614 977.74228
239 3.87207 1006.73716
240 3.83784 993.99952
241 3.69329 952.86856
242 3.67458 944.36732
243 3.62279 927.43475
244 3.76710 960.61101
245 3.71671 944.04536
246 3.71304 939.39836
247 3.83086 965.37546
248 3.68536 925.02636
249 3.72044 930.11100
250 3.66949 913.70276
ac convergence test in progress...
Auto-corr tau/N = [0.06297589 0.06731291 0.05644879]
tau/N <= 0.02 = [False False False]
251 3.99689 991.22847
252 3.75812 928.25465
253 3.67617 904.33708
254 3.85785 945.17399
255 3.76486 918.62560
256 3.81698 927.52638
257 3.74492 906.27064
258 3.66318 882.82566
259 3.63869 873.28440
260 3.63176 867.99088
261 3.67512 874.67761
262 3.67523 871.02856
263 3.69969 873.12613
264 3.77005 885.96269
265 3.67885 860.85113
266 3.68810 859.32823
267 3.66130 849.42206
268 3.81635 881.57708
269 3.77393 868.00321
270 3.73869 856.16116
271 3.69881 843.32777
272 3.70014 839.93246
273 3.67018 829.46158
274 3.69924 832.32922
275 3.66537 821.04355
276 3.91223 872.42774
277 3.76496 835.82179
278 3.77894 835.14596
279 3.65312 803.68618
280 3.68510 807.03646
281 3.68645 803.64566
282 3.78947 822.31521
283 3.74320 808.53142
284 3.72511 800.89887
285 3.72136 796.37104
286 3.82323 814.34842
287 3.72338 789.35698
288 3.69846 780.37590
289 3.66250 769.12521
290 3.87651 810.19038
291 3.70039 769.68112
292 3.66136 757.90069
293 3.74012 770.46493
294 3.68819 756.07997
295 3.77779 770.66977
296 3.66924 744.85613
297 3.78223 764.01107
298 3.75285 754.32385
299 3.71427 742.85460
300 3.81358 758.90341
ac convergence test in progress...
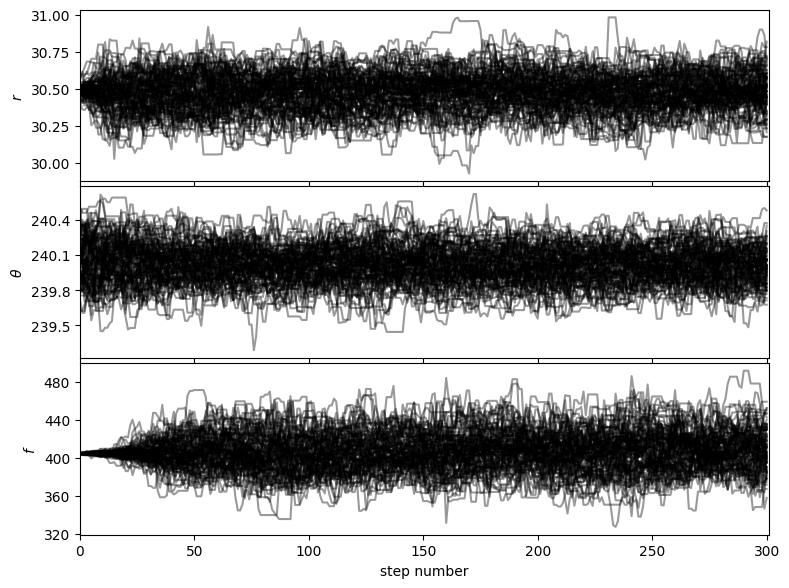
Auto-corr tau/N = [0.05882983 0.06192013 0.05042843]
tau/N <= 0.02 = [False False False]
301 4.28147 847.73086
302 3.84794 758.04339
303 3.70474 726.12865
304 3.81795 744.50064
305 3.72423 722.50004
306 3.68127 710.48434
307 3.70470 711.30182
308 3.80799 727.32628
309 3.73768 710.15863
310 3.70319 699.90367
311 3.71828 699.03589
312 3.78172 707.18127
313 3.83518 713.34255
314 3.82240 707.14382
315 3.74302 688.71531
316 3.83277 701.39673
317 3.74246 681.12772
318 3.73299 675.67155
319 3.74093 673.36704
320 3.69307 661.06043
321 3.67227 653.66406
322 3.72301 658.97312
323 3.72319 655.28197
324 3.75482 657.09332
325 3.68113 640.51575
326 3.82390 661.53418
327 3.67272 631.70836
328 3.66962 627.50434
329 3.65191 620.82402
330 3.68062 622.02410
331 3.68545 619.15594
332 3.81646 637.34815
333 3.81071 632.57753
334 3.74564 618.03076
335 3.68306 604.02233
336 3.81316 621.54459
337 3.82575 619.77118
338 3.82425 615.70425
339 3.86481 618.37024
340 3.74313 595.15703
341 3.72512 588.56975
342 3.96841 623.04053
343 3.74328 583.95230
344 3.73352 578.69514
345 3.68928 568.14912
346 3.73564 571.55338
347 3.76189 571.80758
348 3.73224 563.56779
349 3.74076 561.11460
350 3.71023 552.82457
ac convergence test in progress...
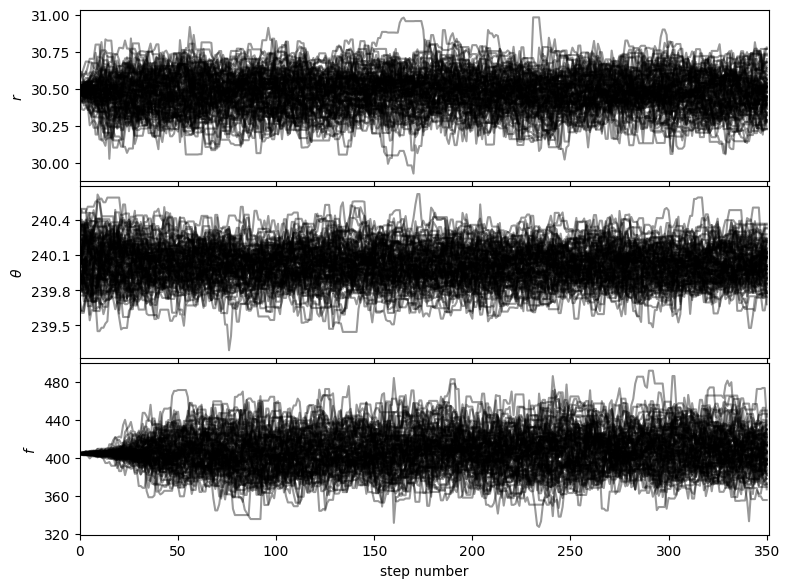
Auto-corr tau/N = [0.05643874 0.05798973 0.04822743]
tau/N <= 0.02 = [False False False]
351 4.45988 660.06268
352 3.98904 586.38917
353 3.66486 535.06912
354 3.67007 532.16044
355 3.64280 524.56291
356 3.70832 530.29033
357 3.71098 526.95959
358 3.66515 516.78671
359 3.72444 521.42104
360 3.71800 516.80242
361 3.78775 522.70964
362 3.72004 509.64575
363 3.72562 506.68446
364 3.74057 504.97735
365 3.76503 504.51415
366 3.77191 501.66416
367 3.76621 497.14038
368 3.75643 492.09168
369 3.67892 478.25960
370 3.68151 474.91518
371 3.68132 471.20858
372 3.79606 482.09987
373 3.75099 472.62461
374 3.71992 464.99000
375 3.73770 463.47530
376 3.97907 489.42549
377 3.76344 459.13980
378 3.67870 445.12222
379 3.65562 438.67380
380 3.72709 443.52312
381 3.72370 439.39648
382 3.67279 429.71666
383 3.65670 424.17662
384 3.83634 441.17899
385 3.66705 418.04359
386 3.77326 426.37827
387 3.90577 437.44646
388 3.80434 422.28196
389 3.68621 405.48255
390 3.70645 404.00349
391 3.86485 417.40337
392 3.77232 403.63856
393 3.80494 403.32396
394 3.73917 392.61275
395 3.64780 379.37130
396 3.71115 382.24804
397 3.94950 402.84931
398 4.00755 404.76275
399 3.96644 396.64420
400 3.87147 383.27573
ac convergence test in progress...
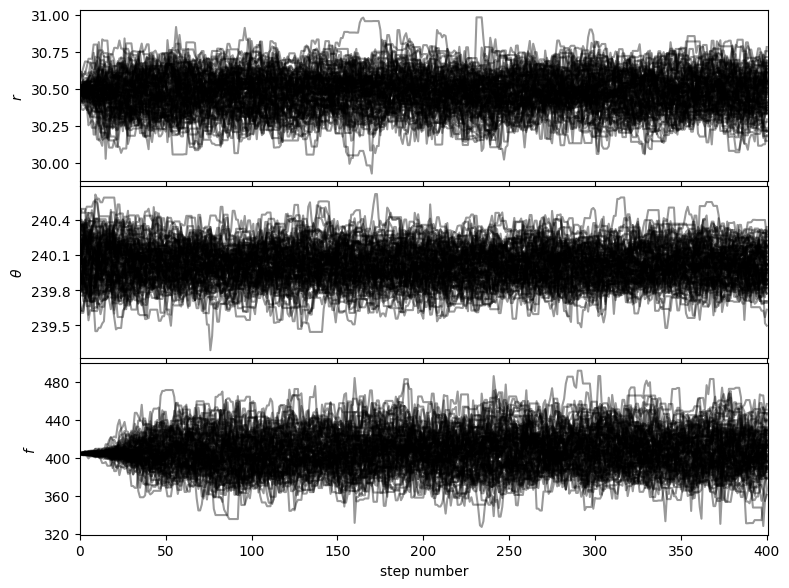
Auto-corr tau/N = [0.05282663 0.05336362 0.04362362]
tau/N <= 0.02 = [False False False]
401 4.26088 417.56644
402 3.78558 367.20107
403 3.77377 362.28144
404 3.67839 349.44676
405 3.74845 352.35439
406 3.65696 340.09691
407 3.70541 340.89754
408 3.68059 334.93387
409 3.65853 329.26770
410 3.78401 336.77725
411 3.79393 333.86549
412 3.84589 334.59226
413 3.86364 332.27278
414 3.74094 317.98007
415 3.88656 326.47087
416 3.86842 321.07878
417 3.77002 309.14139
418 3.85855 312.54255
419 3.73472 298.77792
420 3.72737 294.46223
421 3.72380 290.45609
422 3.67763 283.17736
423 3.76358 286.03208
424 3.69203 276.90202
425 3.67574 272.00476
426 3.89212 284.12476
427 3.91004 281.52281
428 3.84315 272.86393
429 4.11575 288.10243
430 3.75732 259.25515
431 4.09172 278.23703
432 3.90482 261.62314
433 4.03035 266.00317
434 3.79380 246.59687
435 3.94292 252.34720
436 3.81343 240.24584
437 3.85216 238.83417
438 3.67980 224.46792
439 3.73257 223.95432
440 3.81949 225.34997
441 3.75015 217.50876
442 3.73836 213.08652
443 3.77663 211.49117
444 3.74998 206.24912
445 3.84755 207.76748
446 3.88971 206.15452
447 4.13141 214.83327
448 3.73351 190.40881
449 3.92266 196.13310
450 3.90758 191.47122
ac convergence test in progress...
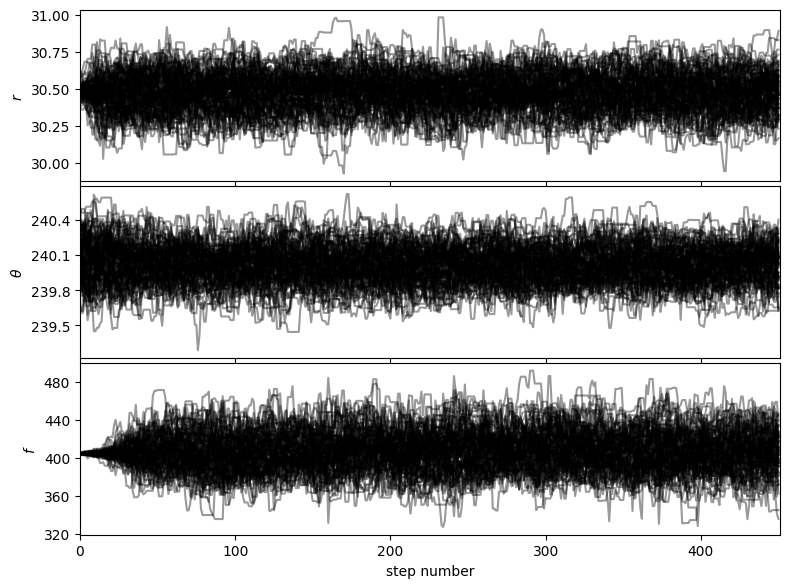
Auto-corr tau/N = [0.04777104 0.0489981 0.04145926]
tau/N <= 0.02 = [False False False]
451 3.97946 191.01418
452 3.70319 174.04988
453 3.74735 172.37819
454 3.75651 169.04290
455 3.67658 161.76930
456 3.66209 157.46991
457 3.95949 166.29841
458 3.65751 149.95799
459 3.84934 153.97360
460 4.09859 159.84485
461 4.10657 156.04951
462 3.99442 147.79350
463 3.74376 134.77518
464 3.78320 132.41193
465 3.80384 129.33059
466 3.85738 127.29364
467 3.77298 120.73526
468 3.67803 114.01896
469 3.81074 114.32226
470 4.12536 119.63553
471 3.75978 105.27387
472 4.01060 108.28615
473 3.83008 99.58216
474 3.86824 96.70610
475 3.73332 89.59973
476 3.78296 87.00813
477 3.72047 81.85034
478 3.75768 78.91128
479 3.70115 74.02304
480 3.71619 70.60767
481 3.71724 66.91030
482 3.68625 62.66622
483 3.69352 59.09638
484 3.74258 56.13869
485 3.70847 51.91857
486 3.69873 48.08353
487 3.70337 44.44050
488 3.70098 40.71081
489 3.77585 37.75854
490 3.77752 33.99772
491 3.77643 30.21140
492 3.77897 26.45283
493 3.77931 22.67584
494 3.96602 19.83009
495 3.78830 15.15322
496 3.69095 11.07284
497 3.72887 7.45774
498 3.72255 3.72255
499 3.68309 0.00000
We have reached the limit # of steps without convergence
Running time: 0:31:28.351899
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
If you ran the previous box and wish to write your results, set write=True in the next box. This will pickle the MCMC chain.
[34]:
write=False
if write:
import pickle
output = {'chain':chain}
with open('../datasets/my_MCMC_results', 'wb') as fileSave:
pickle.dump(output, fileSave)
Pickled results can be loaded from disk like this:
[33]:
import pickle
with open('../datasets/MCMC_results','rb') as fi:
myPickler = pickle.Unpickler(fi)
mcmc_result = myPickler.load()
print(mcmc_result.keys())
chain = mcmc_result['chain']
dict_keys(['chain', 'input_parameters', 'AR', 'lnprobability'])
The most accurate approach would involve setting a large enough maximum number of iterations and using FFT-based rotation for PCA. The latter in particular, may change a bit the most likely parameter values given the better flux conservation. However, these changes would involve over ~3 orders of magnitude longer calculation time. It is therefore intractable for a personal laptop and not shown in this notebook. If you have access to a supercomputer feel free to adopt these changes though. The results after 500 iterations are nonetheless good enough for illustrative purpose:
5.3.3.2. Visualizing the MCMC chain: corner plots and walk plots
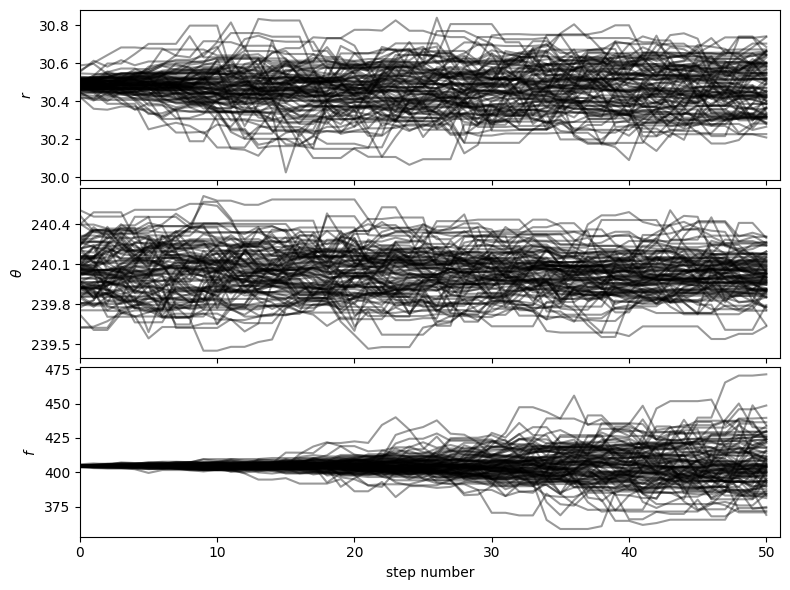
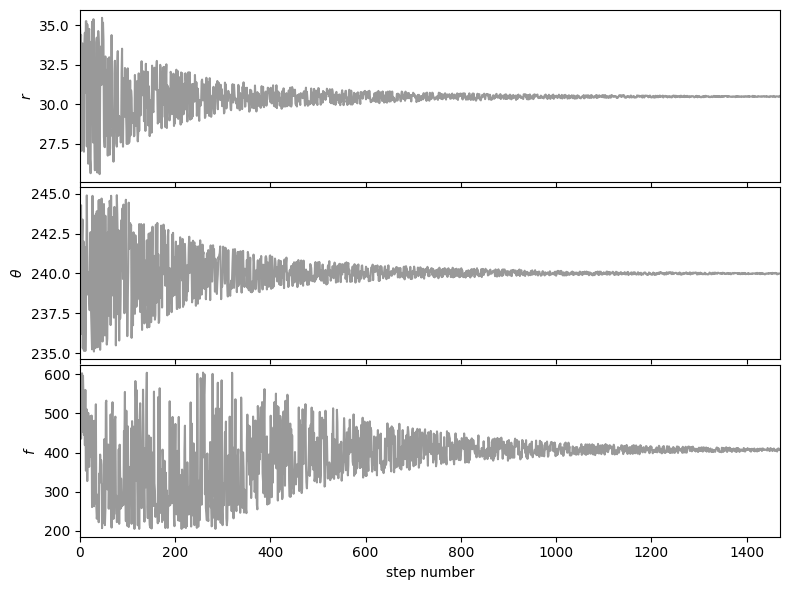
Let’s first check that the walk plots look ok:
[34]:
from vip_hci.fm import show_walk_plot
show_walk_plot(chain)
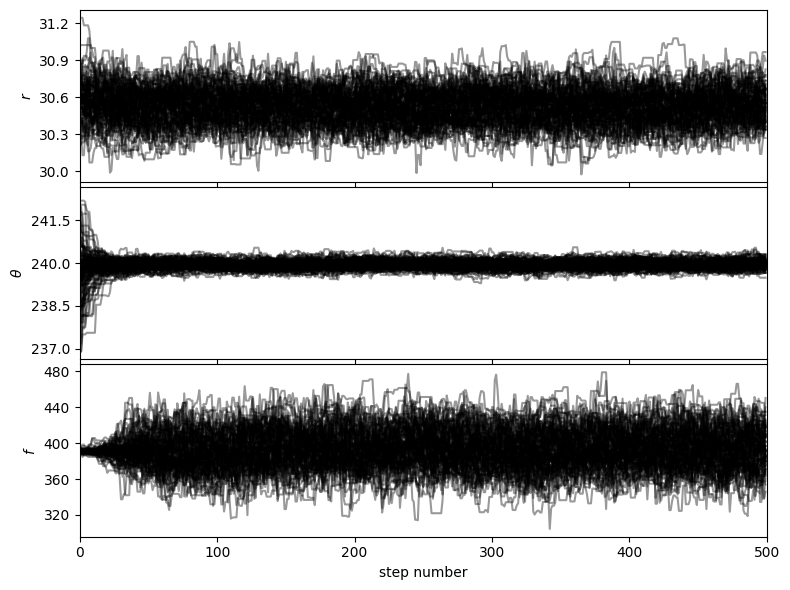
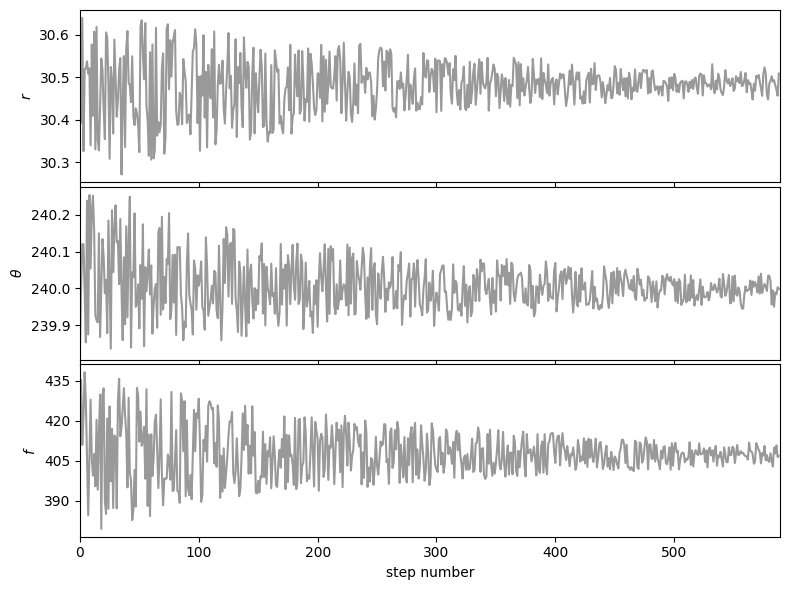
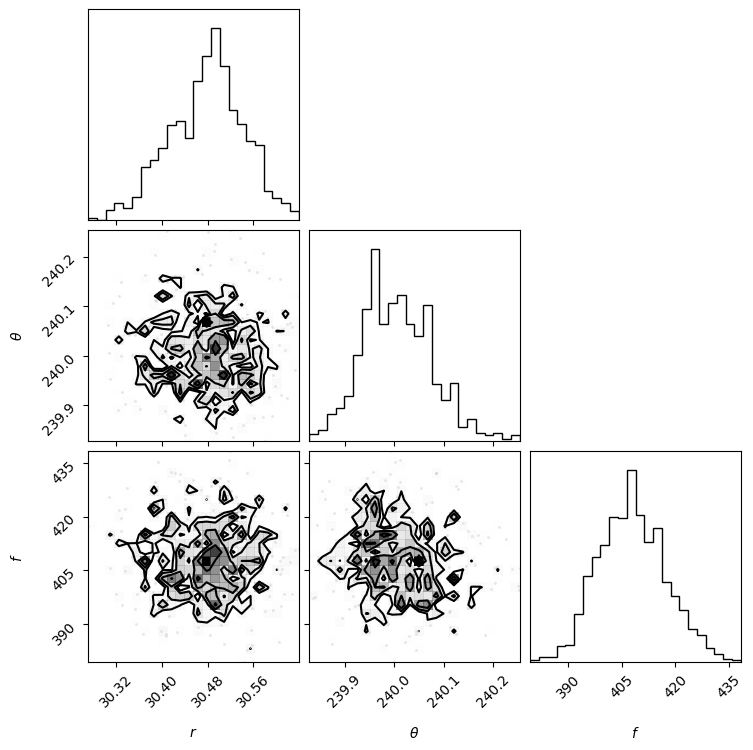
Then based on the walk plot, let’s burn-in the first 30% of the chain (to only keep the iterations where the walkers appear to have mostly converged), to calculate the corner plots:
[35]:
from vip_hci.fm import show_corner_plot
burnin = 0.3
burned_chain = chain[:, int(chain.shape[1]//(1/burnin)):, :]
show_corner_plot(burned_chain)
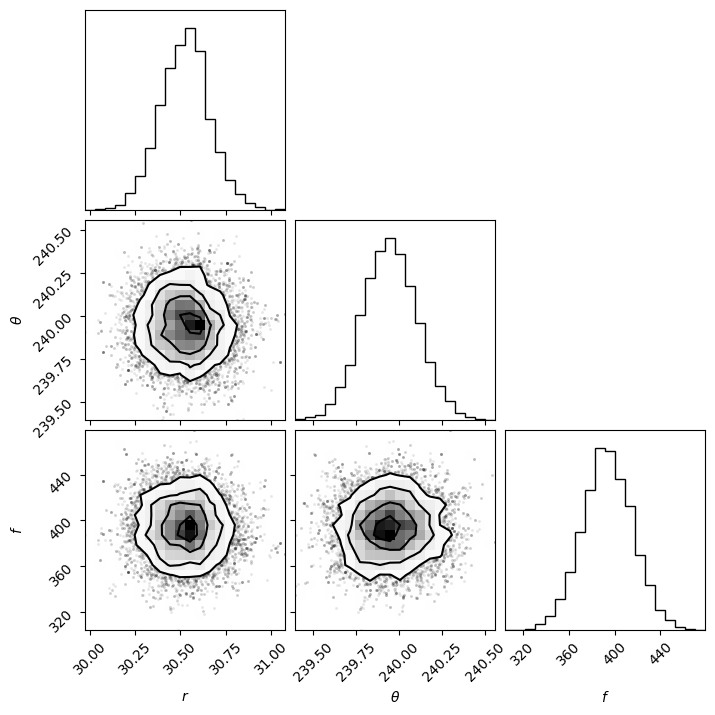
For the purpose of this tutorial and to limit computation time we set the maximum number of iterations to 500 for 100 walkers. The look of the corner plots may improve with more samples (i.e. higher number of iterations, for a given burn-in ratio). This can be tested by setting the max. number of iterations arbitrarily high for the autocorrelation-time convergence criterion to be met.
5.3.3.3. Highly probable values and confidence intervals
Now let’s determine the most highly probable value for each model parameter, as well as the 1-sigma confidence interval. For this, let’s first flatten the chains:
[36]:
isamples_flat = chain[:, int(chain.shape[1]//(1/burnin)):, :].reshape((-1,3))
Then use the confidence function:
[37]:
from vip_hci.fm import confidence
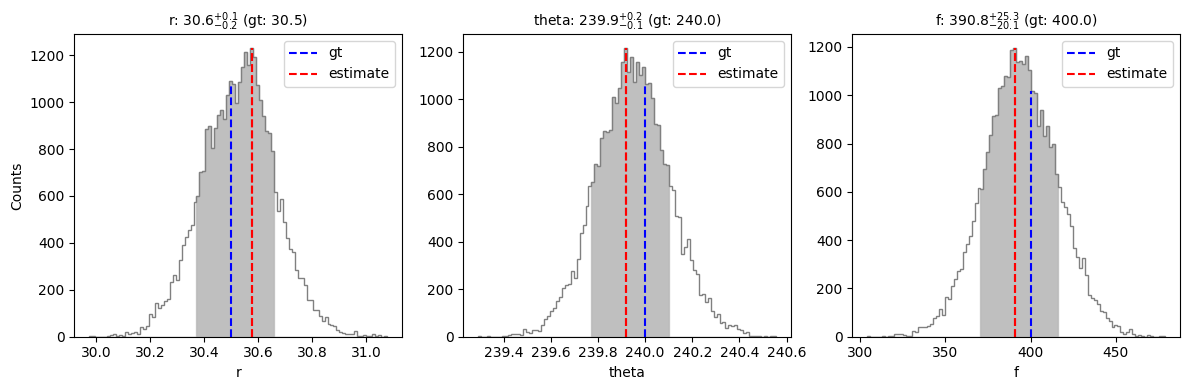
val_max, conf = confidence(isamples_flat, cfd=68, gaussian_fit=False, verbose=True, save=False,
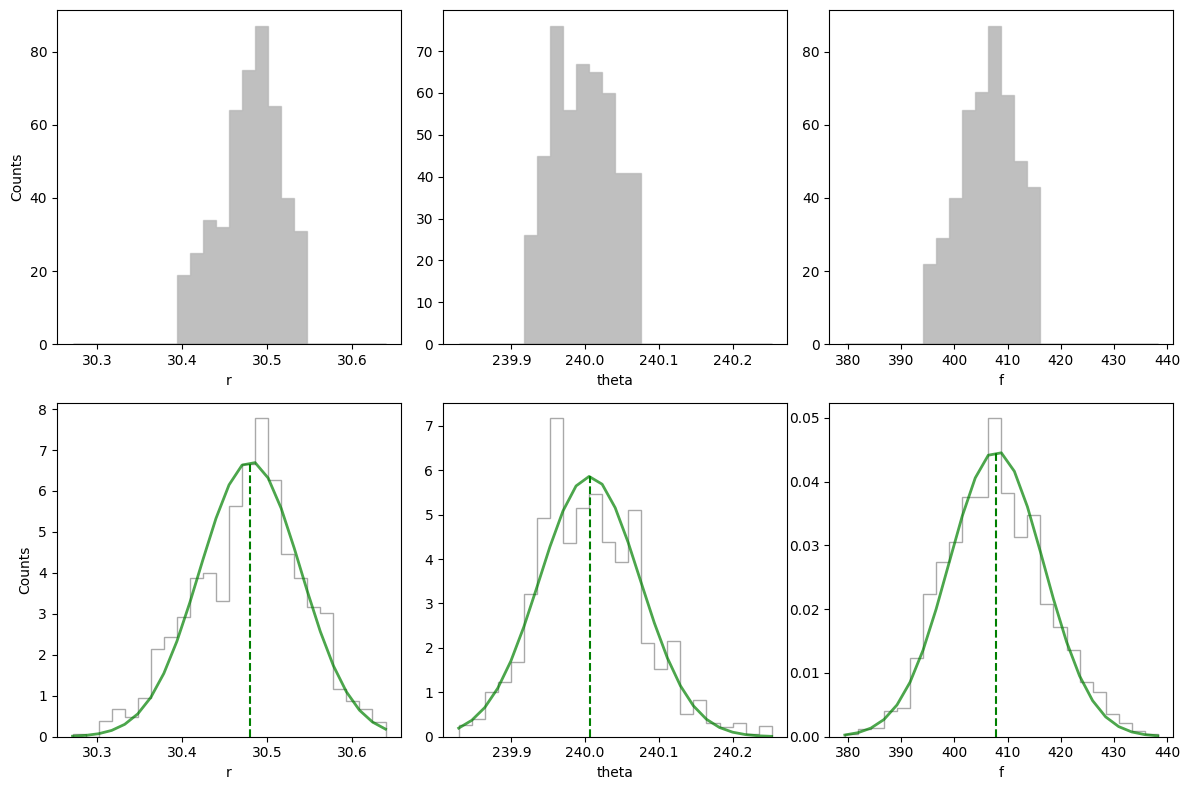
gt=gt, ndig=1, title=True)
percentage for r: 69.79202279202278%
percentage for theta: 69.02279202279202%
percentage for f: 68.94017094017094%
Confidence intervals:
r: 30.57489764243517 [-0.20421878422770945,0.08279139901123145]
theta: 239.91771004343246 [-0.14527599962792692,0.18317408648738365]
f: 390.7650582608513 [-20.054061636888093,25.285555976945886]
Using the confidence function with the gaussian_fit=True option, it is possible to fit a Gaussian to the posterior distribution of each parameter, and infer associated uncertainty values.
[38]:
mu, sigma = confidence(isamples_flat, cfd=68, gaussian_fit=True, verbose=True, save=False,
gt=gt, ndig=1, title=True)
percentage for r: 69.79202279202278%
percentage for theta: 69.02279202279202%
percentage for f: 68.94017094017094%
Confidence intervals:
r: 30.57489764243517 [-0.20421878422770945,0.08279139901123145]
theta: 239.91771004343246 [-0.14527599962792692,0.18317408648738365]
f: 390.7650582608513 [-20.054061636888093,25.285555976945886]
Gaussian fit results:
r: 30.525747462344565 +-0.13676103149725966
theta: 239.94793373875024 +-0.15744912409220196
f: 394.1338634773366 +-21.669634439677626
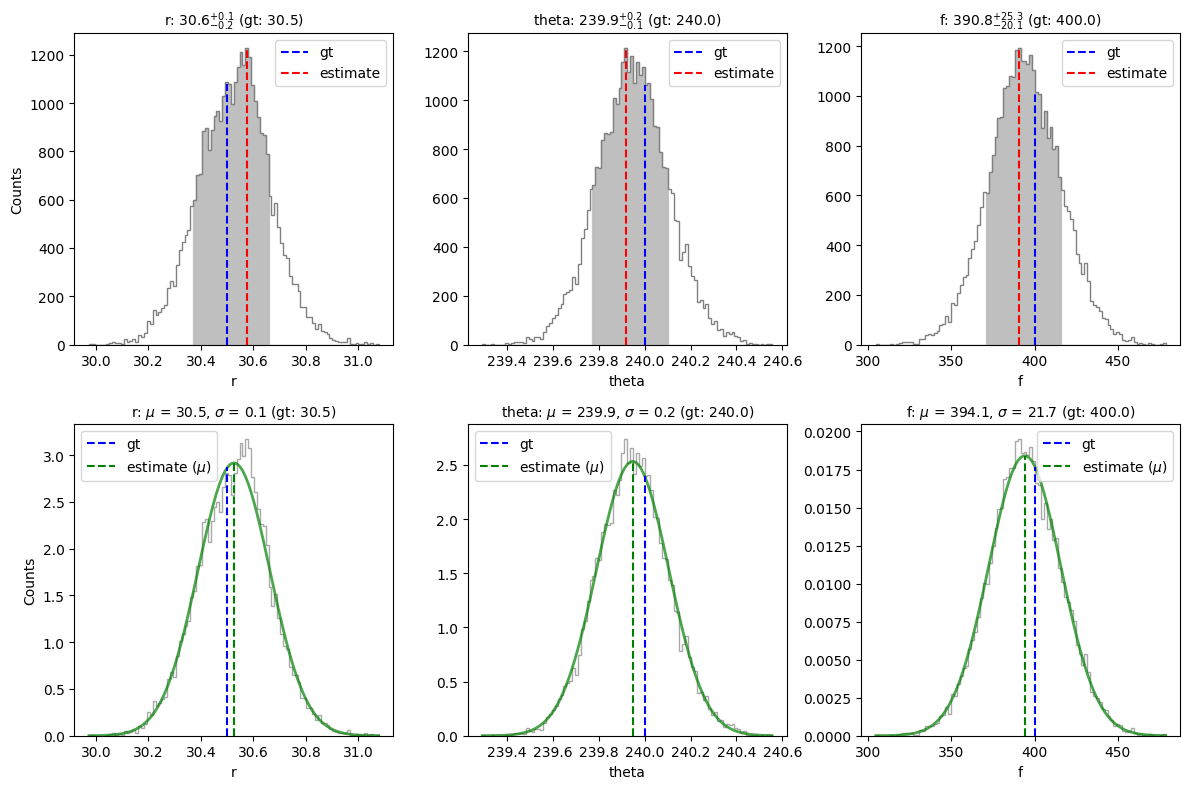
It is recommended to report the results as confidence intervals (i.e. with possibly asymmetric uncertainties) as long as the bin interval is small enough. Here, we also fitted the residual posterior distribution of each parameter to a Gaussian distribution (this shape is the expected one if the noise has been well whitened, but is not necessarily guaranteed at all separations depending on the adopted \(n_{\rm pc}\)). In case these distributions look Gaussian, the inferred \(\sigma\) value may be a more accurate uncertainty value for the different parameters.
We can see that the confidence intervals inferred by NEGFC for the different parameters encompass the ground truth values used for injection (in particular for the flux).
5.3.4. NEGFC technique coupled with nested sampling
Nested sampling can be a faster approach to estimate the optimal parameters, given a good first guess estimate.
The implementation in VIP relies on nestle (Barbary 2013; more details here).
The procedure is essentially the same as for the MCMC sampler. Let’s first set the parameters associated with the observation:
[39]:
obs_params = {'psfn': psfn,
'fwhm': fwhm_naco}
Let’s then set the parameters associated with pca_annulus, the PSF modeling and subtraction algorithm:
[40]:
annulus_width = 4*fwhm_naco
algo_params = {'algo': pca_annulus,
'ncomp': opt_npc_ann,
'annulus_width': annulus_width,
'svd_mode': 'lapack'}
algo_options = {'imlib': imlib_rot,
'interpolation': interpolation}
For a change, let’s consider fmerit='sum' for the choice of log-likelihood expression, hence set mu_sigma=False. Let’s keep an aperture_radius of 2 FWHM.
[41]:
aperture_radius=2
mu_sigma = False
fmerit = 'sum'
negfc_params = {'mu_sigma': mu_sigma,
'fmerit': fmerit,
'aperture_radius': aperture_radius}
Let’s define our first guess on the parameters as the initial_state:
[42]:
initial_state = np.array([r_0[0], theta_0[0], f_0[0]])
Let’s now define the parameters of the nested sampling algorithm. These are a bit different from MCMC:
npointssets the number of live points (similar to walkers in MCMC);dlogzis related to a criterion used to stop the iterations. Iterations will stop when the estimated contribution of the remaining prior volume to the total evidence falls below this threshold. Explicitly, the stopping criterion is log(\(z\) + \(z_{\rm est}\)) - log(\(z\)) < \(dlogz\) where \(z\) is the current evidence from all saved samples, and \(z_{\rm est}\) is the estimated contribution from the remaining volume. Typical good values: 0.1 or 0.5;decline_factoris related to an alternative criterion to stop the iterations. Iterations will stop when the weight (likelihood times prior volume) of newly saved samples has been declining for decline_factor * nsamples consecutive samples. A value of 1.0 yields good results on this dataset.ware the windows that will bound the exploration space for each parameter. These should be provided in the respective units of each input parameter.rstatecan be used to specify a given random state to start with.
[43]:
npoints = 100
dlogz, decline_factor = (0.1, None)
rstate = None
w = (5, 5, 200)
nested_params = {'npoints': nwalkers,
'dlogz': dlogz,
'decline_factor': None,
'rstate': rstate,
'w': w}
Now let’s start the sampler. Note that this step is computer intensive and may take a few minutes to run depending on your machine (but typically goes 4-5x faster than MCMC with 500 iterations considering the aboved parameters).
[44]:
from vip_hci.fm import nested_negfc_sampling
nested_res = nested_negfc_sampling(initial_state, cubefc, angs, **obs_params, **algo_params, algo_options=algo_options,
**negfc_params, **nested_params, verbose=True)
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Starting time: 2024-03-26 01:10:32
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
Prior bounds on parameters:
Radius [25.485108459103685,35.485108459103685]
Theta [235.0305578125488,245.0305578125488]
Flux [204.54399596690672,604.5439959669068]
Using 100 active points
Total running time:
Running time: 0:06:41.569444
――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――――
The results of the nested sampling as stored in a nestle object. The results can be conveniently inferred using the aptly named nested_sampling_results function, which can also write the results (through save and output_dir arguments):
[46]:
from vip_hci.fm import nested_sampling_results
nested_sampling_results(nested_res, burnin=0.6, bins=None, plot=True, save=True, output_dir='../datasets/')
niter: 1370
ncall: 2782
nsamples: 1470
logz: -62.380 +/- 0.306
h: 9.362
Natural log of prior volume and Weight corresponding to each sample
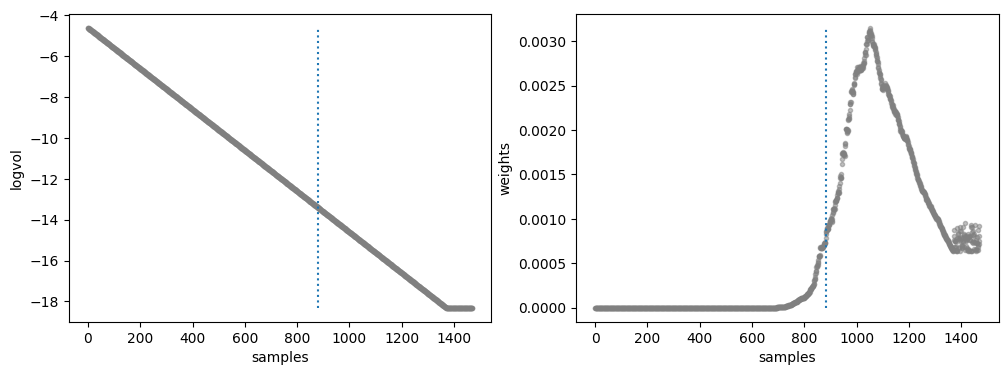
Walk plots before the burnin
Walk plots after the burnin
Weighted mean +- sqrt(covariance)
Radius = 30.479 +/- 0.064
Theta = 240.006 +/- 0.071
Flux = 407.892 +/- 9.386
Hist bins = 24
Confidence intervals
percentage for r: 70.33529165480141%
percentage for theta: 71.59451696713656%
percentage for f: 70.49362534314926%
Confidence intervals:
r: 30.49359600488267 [-0.09972337298495404,0.05369720083805163]
theta: 239.96120315948127 [-0.044221430001499584,0.11497571800393303]
f: 407.60520209708034 [-13.496632905881825,8.588766394652168]
Gaussian fit results:
r: 30.480293430429295 +-0.05934716723598515
theta: 240.0063310083186 +-0.06807952983059093
f: 407.87844951803083 +-8.914065340527006
[46]:
array([[3.04785035e+01, 6.40976163e-02],
[2.40006332e+02, 7.06865973e-02],
[4.07892189e+02, 9.38609668e+00]])
As a reminder the ground truth values are:
[47]:
gt
[47]:
[30.5, 240, 400.0]
The final posterior distributions on the three parameters appear thus reasonable.
5.3.5. Residual speckle uncertainty
Only needed if using ``mu_sigma=False`` in your call to mcmc_negfc_sampling!
Residual speckle noise can bias the best parameter estimates found for the companion (if not taken into account in the MCMC). To evaluate the uncertainty associated to this additional source of noise, it is recommended to inject a large number of fake companions at the same radius and flux as estimated for the true companion but different azimuths, and then estimate their parameters using simplex-NEGFC. The distribution of differences with respect to injected parameters can then give us an idea
of the residual speckle noise uncertainty. This is done in VIP with the speckle_noise_uncertainty function (see also Sec. 3.3 in Wertz et al. 2017 for more details).
Let’s use the planet parameters inferred by the MCMC-NEGFC algorithm:
[48]:
pl_par = (val_max['r'],val_max['theta'],val_max['f'])
pl_par
[48]:
(30.57489764243517, 239.91771004343246, 390.7650582608513)
[49]:
from vip_hci.fm import speckle_noise_uncertainty
algo_options={'ncomp':opt_npc_ann, 'annulus_width':4*fwhm_naco, 'imlib':imlib_rot,
'interpolation':interpolation}
speckle_res = speckle_noise_uncertainty(cubefc, pl_par, np.linspace(0,359,360), angs, pca_annulus,
psfn, fwhm_naco, aperture_radius=2, fmerit='sum',
algo_options=algo_options, transmission=None, mu_sigma=None,
wedge=None, weights=None, force_rPA=False, nproc=None,
simplex_options=None, bins=None, save=False, output=None,
verbose=True, full_output=True, plot=True)
#######################################################
### SPECKLE NOISE DETERMINATION ###
#######################################################
Number of steps: 360
Process is running for angle: 0.00
Process is running for angle: 18.00Process is running for angle: 36.00
Process is running for angle: 54.00
Process is running for angle: 72.00
Process is running for angle: 1.00
Process is running for angle: 19.00
Process is running for angle: 73.00
Process is running for angle: 37.00
Process is running for angle: 55.00
Process is running for angle: 2.00
Process is running for angle: 74.00
Process is running for angle: 38.00
Process is running for angle: 20.00
Process is running for angle: 56.00
Process is running for angle: 75.00
Process is running for angle: 3.00
Process is running for angle: 39.00
Process is running for angle: 57.00
Process is running for angle: 21.00
Process is running for angle: 4.00
Process is running for angle: 76.00
Process is running for angle: 40.00
Process is running for angle: 22.00
Process is running for angle: 58.00
Process is running for angle: 5.00
Process is running for angle: 41.00
Process is running for angle: 77.00
Process is running for angle: 59.00
Process is running for angle: 23.00
Process is running for angle: 6.00
Process is running for angle: 78.00
Process is running for angle: 42.00
Process is running for angle: 24.00
Process is running for angle: 60.00
Process is running for angle: 7.00
Process is running for angle: 79.00
Process is running for angle: 25.00
Process is running for angle: 43.00
Process is running for angle: 61.00
Process is running for angle: 80.00
Process is running for angle: 8.00
Process is running for angle: 44.00
Process is running for angle: 26.00
Process is running for angle: 62.00
Process is running for angle: 81.00
Process is running for angle: 45.00
Process is running for angle: 27.00
Process is running for angle: 9.00
Process is running for angle: 63.00
Process is running for angle: 28.00
Process is running for angle: 82.00
Process is running for angle: 46.00
Process is running for angle: 10.00
Process is running for angle: 64.00
Process is running for angle: 29.00
Process is running for angle: 47.00
Process is running for angle: 83.00
Process is running for angle: 11.00
Process is running for angle: 30.00
Process is running for angle: 65.00
Process is running for angle: 84.00
Process is running for angle: 48.00
Process is running for angle: 12.00
Process is running for angle: 85.00
Process is running for angle: 31.00
Process is running for angle: 66.00
Process is running for angle: 49.00
Process is running for angle: 13.00
Process is running for angle: 86.00
Process is running for angle: 32.00
Process is running for angle: 67.00
Process is running for angle: 14.00
Process is running for angle: 50.00
Process is running for angle: 87.00
Process is running for angle: 33.00
Process is running for angle: 68.00
Process is running for angle: 51.00
Process is running for angle: 15.00
Process is running for angle: 88.00
Process is running for angle: 34.00
Process is running for angle: 69.00
Process is running for angle: 16.00
Process is running for angle: 52.00
Process is running for angle: 89.00
Process is running for angle: 35.00
Process is running for angle: 70.00
Process is running for angle: 17.00
Process is running for angle: 53.00
Process is running for angle: 90.00
Process is running for angle: 71.00
Process is running for angle: 108.00
Process is running for angle: 126.00
Process is running for angle: 144.00
Process is running for angle: 91.00
Process is running for angle: 109.00
Process is running for angle: 127.00
Process is running for angle: 162.00
Process is running for angle: 145.00
Process is running for angle: 92.00
Process is running for angle: 128.00
Process is running for angle: 110.00
Process is running for angle: 163.00
Process is running for angle: 146.00
Process is running for angle: 93.00
Process is running for angle: 111.00
Process is running for angle: 129.00
Process is running for angle: 147.00
Process is running for angle: 164.00
Process is running for angle: 94.00
Process is running for angle: 130.00
Process is running for angle: 148.00
Process is running for angle: 112.00
Process is running for angle: 165.00
Process is running for angle: 95.00
Process is running for angle: 131.00
Process is running for angle: 113.00
Process is running for angle: 149.00
Process is running for angle: 166.00
Process is running for angle: 132.00
Process is running for angle: 96.00
Process is running for angle: 150.00
Process is running for angle: 114.00
Process is running for angle: 133.00
Process is running for angle: 167.00
Process is running for angle: 151.00
Process is running for angle: 97.00
Process is running for angle: 115.00
Process is running for angle: 134.00
Process is running for angle: 168.00
Process is running for angle: 152.00
Process is running for angle: 98.00
Process is running for angle: 116.00
Process is running for angle: 135.00
Process is running for angle: 169.00
Process is running for angle: 99.00
Process is running for angle: 153.00
Process is running for angle: 117.00
Process is running for angle: 136.00
Process is running for angle: 170.00
Process is running for angle: 154.00
Process is running for angle: 100.00
Process is running for angle: 118.00
Process is running for angle: 137.00
Process is running for angle: 101.00
Process is running for angle: 171.00
Process is running for angle: 119.00
Process is running for angle: 155.00
Process is running for angle: 138.00
Process is running for angle: 172.00
Process is running for angle: 102.00
Process is running for angle: 120.00
Process is running for angle: 156.00
Process is running for angle: 139.00
Process is running for angle: 103.00
Process is running for angle: 173.00
Process is running for angle: 157.00
Process is running for angle: 121.00
Process is running for angle: 140.00
Process is running for angle: 174.00
Process is running for angle: 158.00
Process is running for angle: 104.00
Process is running for angle: 122.00
Process is running for angle: 141.00
Process is running for angle: 159.00
Process is running for angle: 105.00
Process is running for angle: 175.00
Process is running for angle: 123.00
Process is running for angle: 142.00
Process is running for angle: 160.00
Process is running for angle: 106.00
Process is running for angle: 176.00
Process is running for angle: 124.00
Process is running for angle: 143.00
Process is running for angle: 107.00
Process is running for angle: 161.00
Process is running for angle: 177.00
Process is running for angle: 125.00
Process is running for angle: 180.00
Process is running for angle: 198.00
Process is running for angle: 216.00
Process is running for angle: 178.00
Process is running for angle: 234.00
Process is running for angle: 181.00
Process is running for angle: 199.00
Process is running for angle: 217.00
Process is running for angle: 179.00
Process is running for angle: 235.00
Process is running for angle: 182.00
Process is running for angle: 200.00
Process is running for angle: 252.00
Process is running for angle: 218.00
Process is running for angle: 236.00
Process is running for angle: 183.00
Process is running for angle: 201.00
Process is running for angle: 253.00
Process is running for angle: 219.00
Process is running for angle: 237.00
Process is running for angle: 184.00
Process is running for angle: 202.00
Process is running for angle: 254.00
Process is running for angle: 220.00
Process is running for angle: 185.00
Process is running for angle: 238.00
Process is running for angle: 203.00
Process is running for angle: 255.00
Process is running for angle: 221.00
Process is running for angle: 186.00
Process is running for angle: 239.00
Process is running for angle: 204.00
Process is running for angle: 222.00
Process is running for angle: 256.00
Process is running for angle: 240.00
Process is running for angle: 187.00
Process is running for angle: 205.00
Process is running for angle: 257.00
Process is running for angle: 223.00
Process is running for angle: 188.00
Process is running for angle: 241.00
Process is running for angle: 258.00
Process is running for angle: 224.00
Process is running for angle: 206.00
Process is running for angle: 189.00
Process is running for angle: 242.00
Process is running for angle: 190.00
Process is running for angle: 259.00
Process is running for angle: 225.00
Process is running for angle: 207.00
Process is running for angle: 243.00
Process is running for angle: 191.00
Process is running for angle: 226.00
Process is running for angle: 244.00
Process is running for angle: 208.00
Process is running for angle: 260.00
Process is running for angle: 227.00
Process is running for angle: 192.00
Process is running for angle: 209.00
Process is running for angle: 245.00
Process is running for angle: 261.00
Process is running for angle: 193.00
Process is running for angle: 228.00
Process is running for angle: 210.00
Process is running for angle: 246.00
Process is running for angle: 262.00
Process is running for angle: 229.00
Process is running for angle: 211.00
Process is running for angle: 194.00
Process is running for angle: 247.00
Process is running for angle: 263.00
Process is running for angle: 230.00
Process is running for angle: 195.00
Process is running for angle: 212.00
Process is running for angle: 248.00
Process is running for angle: 264.00
Process is running for angle: 196.00
Process is running for angle: 231.00
Process is running for angle: 249.00
Process is running for angle: 213.00
Process is running for angle: 265.00
Process is running for angle: 197.00
Process is running for angle: 250.00
Process is running for angle: 232.00
Process is running for angle: 214.00
Process is running for angle: 266.00
Process is running for angle: 270.00
Process is running for angle: 233.00
Process is running for angle: 251.00
Process is running for angle: 215.00
Process is running for angle: 271.00
Process is running for angle: 267.00
Process is running for angle: 288.00
Process is running for angle: 306.00
Process is running for angle: 324.00
Process is running for angle: 268.00
Process is running for angle: 272.00
Process is running for angle: 289.00
Process is running for angle: 307.00
Process is running for angle: 325.00
Process is running for angle: 269.00
Process is running for angle: 273.00
Process is running for angle: 290.00
Process is running for angle: 326.00
Process is running for angle: 308.00
Process is running for angle: 342.00
Process is running for angle: 274.00
Process is running for angle: 327.00
Process is running for angle: 291.00
Process is running for angle: 309.00
Process is running for angle: 275.00
Process is running for angle: 343.00
Process is running for angle: 328.00
Process is running for angle: 310.00
Process is running for angle: 292.00
Process is running for angle: 276.00
Process is running for angle: 329.00
Process is running for angle: 344.00
Process is running for angle: 311.00
Process is running for angle: 293.00
Process is running for angle: 277.00
Process is running for angle: 330.00
Process is running for angle: 345.00
Process is running for angle: 278.00
Process is running for angle: 312.00
Process is running for angle: 294.00
Process is running for angle: 331.00
Process is running for angle: 346.00
Process is running for angle: 279.00
Process is running for angle: 313.00
Process is running for angle: 295.00
Process is running for angle: 332.00
Process is running for angle: 280.00
Process is running for angle: 347.00
Process is running for angle: 314.00
Process is running for angle: 333.00
Process is running for angle: 281.00
Process is running for angle: 348.00
Process is running for angle: 315.00
Process is running for angle: 296.00
Process is running for angle: 334.00
Process is running for angle: 282.00
Process is running for angle: 349.00
Process is running for angle: 316.00
Process is running for angle: 297.00
Process is running for angle: 335.00
Process is running for angle: 283.00
Process is running for angle: 298.00
Process is running for angle: 350.00
Process is running for angle: 317.00
Process is running for angle: 336.00
Process is running for angle: 284.00
Process is running for angle: 299.00
Process is running for angle: 351.00
Process is running for angle: 318.00
Process is running for angle: 337.00
Process is running for angle: 300.00
Process is running for angle: 285.00
Process is running for angle: 319.00
Process is running for angle: 338.00
Process is running for angle: 352.00
Process is running for angle: 339.00
Process is running for angle: 301.00
Process is running for angle: 286.00
Process is running for angle: 320.00
Process is running for angle: 353.00
Process is running for angle: 302.00
Process is running for angle: 287.00
Process is running for angle: 340.00
Process is running for angle: 321.00
Process is running for angle: 354.00
Process is running for angle: 303.00
Process is running for angle: 341.00
Process is running for angle: 322.00
Process is running for angle: 355.00
Process is running for angle: 304.00
Process is running for angle: 323.00
Process is running for angle: 356.00
Process is running for angle: 305.00
Process is running for angle: 357.00
Process is running for angle: 358.00
Process is running for angle: 359.00
residuals (offsets): [-0.07194726 -0.0679137 -0.05284979 -0.04923129 -0.03134428 -0.02385255
-0.02770335 -0.01316644 0.0272692 0.03564376 0.06143588 0.09204717
0.06127146 0.02996715 -0.01622812 0.022861 -0.0219606 -0.02613912
-0.02893477 -0.02928718 -0.06395122 -0.01972318 -0.01405615 -0.01428813
-0.01221347 -0.0091661 0.00397442 0.02939105 0.07737107 0.07793074
0.06939257 0.09053146 0.05039821 0.03183504 0.01349798 0.00373654
-0.02376855 -0.02876652 -0.01368514 0.04727208 0.03718008 0.0564711
0.04430948 0.00173693 -0.0002993 -0.05071577 -0.02567797 -0.03166467
0.00631743 0.00938794 -0.00834402 0.00956522 -0.04283893 -0.05242955
-0.0206909 -0.02133019 0.019542 0.01061824 -0.01490506 -0.02449045
-0.02184346 0.00183338 -0.00278437 0.01424072 0.03277652 0.04592176
0.05601213 0.08424237 0.08633189 0.12877568 0.09227417 0.07736753
0.05146104 0.02048522 -0.04877792 -0.09115308 -0.12909214 -0.10102868
-0.09161111 -0.04142226 -0.04221879 -0.02010684 -0.04001772 -0.0345262
-0.00623193 -0.02041676 -0.017747 -0.00693992 0.00873011 0.00768424
0.00217757 0.03739337 0.07481452 0.09930407 0.09406576 0.06629036
0.03532193 0.05337189 0.02682115 0.00961366 -0.00946944 -0.01135301
-0.02652141 -0.03899544 -0.05629713 -0.05895856 -0.07139986 -0.04544512
-0.06271726 -0.02774389 0.02468827 0.05123639 0.05123394 0.067893
0.07151009 0.08143657 0.11102183 0.05354179 0.026072 0.0048551
0.01139111 -0.0133471 -0.04794281 -0.03418549 -0.04433242 -0.03333279
-0.03644418 -0.02508181 -0.01790369 -0.02305647 -0.00125149 0.05014574
0.04115926 0.06967283 0.07185054 0.08211495 0.07341343 0.07399687
0.05759923 0.06494044 0.04043134 0.00213029 -0.02681872 -0.0589104
-0.10728953 -0.1174301 -0.09815653 -0.11151935 -0.03738393 0.02308855
0.0483004 0.05255399 0.07235345 0.09472702 0.05416526 0.10981192
0.05589724 -0.03063201 -0.05369212 -0.06221116 -0.14412857 -0.10137107
-0.10206328 -0.07055895 -0.05358256 -0.02228003 -0.02206437 0.02954577
0.03822636 0.09898593 0.11131464 0.10517388 0.09698835 0.05623946
0.05736546 0.04320881 -0.04203858 -0.04568166 -0.05966887 -0.05361753
-0.05196568 -0.04837144 -0.07490089 -0.04922966 -0.04519586 -0.05233578
-0.00201623 0.00825943 0.00835011 0.01043159 0.01603433 0.00259533
0.01970656 -0.0007763 -0.00483066 -0.00324009 -0.01425677 0.00892762
0.00103555 0.03648212 0.02478722 0.02996958 0.04928787 0.05135024
0.08658284 0.10554381 0.09648956 0.12604682 0.13011816 0.09306574
0.001344 -0.04732511 -0.06118338 -0.07463597 -0.06611751 -0.10314761
-0.12428097 -0.09853047 -0.0833209 -0.05468985 -0.02267745 -0.0440875
-0.00983378 0.0034953 0.00376758 0.00730973 0.06302082 0.06689087
0.073345 0.07523411 0.08158614 0.0970739 0.10487012 0.10120079
0.01577984 -0.02067154 -0.02442544 -0.03602889 -0.04547055 -0.08414107
-0.11448931 -0.12591055 -0.1281402 -0.10916153 -0.04709825 -0.04523501
-0.0273786 0.00960444 0.0336095 0.05267335 0.096269 0.11350739
0.10038406 0.07060599 0.06824134 0.02929854 0.00656048 0.00513434
-0.0360569 -0.03369766 -0.04887169 -0.0638559 -0.10347281 -0.100719
-0.10523117 -0.07196939 -0.06712754 -0.06282699 0.00723172 -0.00217401
0.04317411 0.05060612 0.06511812 0.08594664 0.1028961 0.07371741
0.03305175 0.02315862 0.0102798 0.00739765 -0.01273748 -0.05773201
-0.0725282 -0.00946096 -0.03338557 -0.0140088 -0.01565013 0.00872244
0.00447602 0.0178273 0.01917464 0.05143419 -0.00476554 0.05515255
-0.00483736 -0.01437873 -0.03674513 -0.04201056 -0.03738895 -0.07856279
-0.04594965 -0.04187232 -0.0115251 -0.00415247 -0.011091 0.04294494
0.04648292 0.00693908 0.00313017 0.02102484 -0.01832223 -0.02817719
-0.00981371 -0.02354711 -0.02368294 -0.02079812 -0.02166621 0.01916228
-0.02127231 0.01210462 -0.02700047 0.0094098 0.00633137 0.00550697
-0.01750986 -0.01004689 -0.00535751 -0.03439228 -0.03913266 -0.04520319
-0.04624407 -0.0360385 -0.01226754 -0.01126822 -0.00967491 -0.00067078
-0.02739939 -0.01298944 -0.0376359 -0.05840249 -0.04907031 -0.08541701
-0.05737623 -0.03797939 0.00146497 0.01641732 0.06884748 0.07475891
0.13219938 0.14263551 0.1057899 0.09961211 0.10197534 0.08381953
0.05856987 0.01539992 0.01412618 -0.00638121 -0.03685427 -0.06528263] [ 4.39589985e-04 6.39540190e-02 5.98267823e-02 9.50523138e-02
1.06251649e-01 7.70431000e-02 7.13876219e-02 6.61607813e-02
4.42678115e-02 2.35712229e-02 -3.19667221e-02 -3.66466839e-02
-5.08026376e-02 -6.61005769e-02 -5.68134145e-02 -5.40338084e-02
1.70978366e-02 2.63123598e-02 2.85330983e-02 3.35454551e-02
2.80137845e-02 -1.35520724e-03 1.00915290e-02 4.18867305e-03
-3.62817333e-04 -9.45795195e-03 -1.44974539e-02 2.52894714e-03
-4.02000918e-02 -5.28320215e-02 -5.31471476e-02 -6.25454781e-02
-4.58053862e-02 -3.05076369e-02 -6.52762219e-02 -2.99792177e-02
-1.05164759e-02 5.39183818e-02 4.87762130e-02 5.68818136e-02
7.70450123e-02 5.57966391e-02 4.71441011e-02 1.16752923e-02
7.84834822e-03 -7.76514293e-02 -7.90036913e-02 -1.22556364e-01
-1.11322369e-01 -1.10589705e-01 -1.15674680e-01 -1.26066563e-03
7.07734105e-02 1.00159128e-01 2.14030684e-01 2.19779253e-01
1.59313850e-01 1.38972997e-01 3.12908505e-02 -2.75149698e-02
-7.82405468e-02 -1.23011492e-01 -1.63575673e-01 -1.56674850e-01
-1.68881714e-01 -9.71079925e-02 -8.18778406e-02 -4.85161986e-04
2.25582450e-02 1.41262825e-02 2.54004193e-02 4.00614653e-02
-3.27730757e-03 -5.03242426e-02 6.98219439e-03 5.74026731e-02
7.50871846e-02 1.25986002e-01 1.53290431e-01 1.11909853e-01
1.23995222e-01 8.85942000e-02 4.28189876e-02 -1.84346409e-03
-4.88546351e-02 -8.78134045e-02 -9.78389969e-02 -7.78465143e-02
-1.08609767e-01 -9.34414184e-02 -1.44027557e-02 3.81142202e-02
9.53756810e-02 6.52000690e-02 8.10723316e-02 2.20837469e-02
4.35510967e-02 1.23603446e-04 -2.72791632e-03 -5.19439312e-02
-2.36916688e-02 -1.88753218e-02 -8.79241039e-03 -1.72402522e-02
-1.58529775e-02 -1.08866110e-02 1.32699684e-02 3.58795393e-03
9.17962680e-03 6.51572873e-02 7.51058338e-02 4.05078531e-02
4.02292921e-02 -3.50031482e-03 -4.59620503e-02 -5.41212806e-02
-5.76880265e-02 -4.75138600e-02 -4.78030643e-02 -3.23927023e-02
2.27142094e-02 -2.17339029e-02 -1.04610227e-02 -3.18253175e-03
8.72653194e-03 -3.67822185e-03 1.03536754e-02 5.37323341e-02
5.78887958e-02 3.53628803e-02 3.87444693e-02 1.73485109e-02
-1.21554862e-02 -3.36273861e-02 -4.97471366e-02 -1.37489360e-02
1.20706524e-02 3.50303988e-02 6.07347952e-02 1.14537189e-03
1.58955610e-02 4.17837900e-02 -1.53592087e-02 -5.70074377e-02
-9.18158239e-02 -8.22800272e-02 -8.47346524e-02 -4.24421221e-02
4.93421890e-02 8.54698493e-02 9.80986607e-02 6.34094675e-02
1.11664121e-01 1.05455979e-01 1.79742020e-02 3.98566832e-02
-2.02393594e-02 -6.75153121e-02 -4.79413155e-02 -4.40625340e-03
-1.34332515e-02 2.89408292e-02 6.30505848e-02 -1.25430275e-02
-4.21589312e-02 -1.31559619e-01 -1.23955410e-01 -5.86366147e-02
-4.50332644e-02 -6.86271174e-03 -1.67580888e-02 1.19723346e-02
3.44927323e-02 5.95894739e-02 5.88487924e-02 3.58163057e-02
4.21725187e-02 4.21002248e-02 1.91076210e-02 -9.15186235e-03
-2.16819417e-02 -4.54055868e-02 -4.77298422e-02 -4.71459232e-02
-3.09562714e-02 -3.22743021e-02 2.36877396e-02 5.77815926e-02
5.49355249e-02 5.78180344e-02 4.85962475e-02 3.95446909e-02
1.64714383e-02 1.81615884e-02 1.23208380e-02 1.11255234e-02
1.26948481e-02 3.79876915e-02 8.31776617e-02 4.96106895e-02
3.34279243e-02 -1.60696654e-02 -2.90663208e-04 -1.24671275e-01
-1.48102533e-01 -1.79105393e-01 -1.57216943e-01 -9.60387074e-02
-4.89420517e-02 -2.25632453e-03 4.10460314e-02 6.22352176e-02
8.81079260e-02 1.23552824e-01 1.28332011e-01 1.39369411e-01
8.70261061e-02 6.73782071e-02 3.82990422e-02 2.57481197e-02
-1.20562034e-02 -5.37271567e-02 -5.96661609e-02 -8.12333682e-02
-1.17536223e-01 -1.29832894e-01 -1.18646347e-01 -1.48379555e-01
-1.41501197e-01 -1.25584407e-01 -1.30768103e-01 1.32358361e-02
3.66122855e-02 8.52408495e-02 1.59808681e-01 1.61741336e-01
1.39457242e-01 1.74126956e-01 1.30631191e-01 8.22601422e-02
8.76183718e-02 7.23641766e-02 1.74537262e-02 3.08023795e-02
-1.48412961e-03 -3.06580416e-02 -8.51727014e-02 -1.26686385e-01
-9.71313608e-02 -1.22994090e-01 -1.23328563e-01 -1.79197846e-02
-2.60654254e-02 -4.20646620e-02 -2.32701776e-02 -2.21050941e-02
2.60905185e-03 3.73589103e-02 5.41576886e-02 8.36495693e-02
8.98420972e-02 9.72865592e-02 4.40331795e-02 8.68902907e-03
-2.28778486e-02 -1.62994762e-02 -5.57823588e-02 -3.19699735e-02
2.44127104e-02 2.55124186e-02 4.96348703e-02 6.16594690e-02
5.37886968e-02 5.64369464e-02 4.40115426e-02 4.07741391e-02
5.39407031e-04 -1.61196871e-02 -3.32612218e-02 -7.31180562e-02
-6.57773859e-02 -7.30532220e-02 -6.28880150e-02 -2.02230941e-02
-8.73082243e-03 7.33599425e-03 3.13597410e-02 6.56435333e-02
7.34802975e-02 1.04778825e-01 8.68597731e-02 5.41558311e-02
3.09254483e-02 6.36764333e-02 -4.53080547e-02 -8.29481890e-02
-1.17825634e-01 -1.45847273e-01 -1.62576236e-01 -1.36451885e-01
-6.52740340e-02 -2.07944271e-02 1.05285628e-02 9.76243931e-02
1.10883127e-01 1.11983455e-01 9.23336235e-02 6.12695066e-02
5.64372671e-02 2.92004201e-02 4.78338247e-02 2.78977280e-02
-5.44096009e-03 -1.01048764e-02 -1.52609400e-02 -3.03949251e-02
-3.27419762e-02 -9.03091884e-03 3.29404554e-02 4.46135901e-02
2.66133857e-02 -1.68352353e-04 -3.20422225e-02 -5.88810697e-02
-6.42113629e-02 -8.15041842e-02 -8.44044363e-02 -4.85786709e-02
-3.16479814e-02 -2.76331086e-02 -4.57023953e-03 -4.17722380e-03
2.20373514e-02 2.88078078e-03 7.19802275e-05 -6.09123539e-03
-2.25918803e-02 -2.62183842e-02 -3.81123779e-02 -4.68696162e-02
-1.27766754e-02 3.48040056e-02 6.45417061e-02 9.72308514e-02
9.43437348e-02 7.90818361e-02 4.89372700e-02 1.42221551e-02
2.22280066e-02 -1.49605916e-02 -5.66431026e-02 -8.44956136e-02
-7.61184017e-02 -5.88657980e-02 -7.29763790e-02 -5.61712888e-02
-3.95362375e-02 -1.52709465e-03 9.68125944e-03 3.81614762e-02] [-12.64970877 -12.45118743 -7.41837614 -5.07688697 -0.26436484
3.57829826 5.72112899 12.93039223 15.6537636 19.27298956
14.88127936 12.08752188 9.88183297 9.53296132 4.78185878
2.43350404 1.45479044 1.67234378 3.01677196 3.41551738
5.28480538 3.42547286 2.88311864 3.04537626 3.0346159
3.35687866 2.78329156 3.77989787 1.83635521 0.32184025
-2.0498525 -4.37843188 -5.35892736 -6.05988473 -6.13665412
-7.6110908 -6.34181253 -5.22070829 -4.57834615 -3.55303219
4.6745997 4.76444943 5.72549653 -0.27647418 1.16794929
-0.25604996 -2.22055625 0.76514733 -13.07681813 -19.96608498
-36.5027501 -24.11627968 -33.15390158 -18.86319414 -18.42996489
-4.68067572 4.86335107 10.60048471 25.87118991 25.10391634
20.25243155 13.75232862 8.52669202 3.53418184 -4.94776727
-13.1307823 -14.34872251 -16.63554436 -15.31429148 -15.38519259
-19.38635063 -19.08676683 -16.34999011 -12.75381024 -17.1134693
-13.91506411 -9.2054056 -6.6139936 2.10865757 4.08564718
10.45497193 11.27096222 17.42849242 18.17835758 12.71295743
11.56012443 7.97842444 0.75076225 -4.89468996 -8.98111678
-7.33783667 -8.88780347 -8.4055664 -9.19644084 -9.46411627
-2.90515592 -0.38662301 -2.12032323 0.69334495 -4.29383089
-2.03273211 -2.30596871 -2.6683452 -2.73300357 -3.00597335
-3.52264336 0.3770185 1.41483411 2.71495332 4.50202613
6.70125735 4.00901286 6.20360334 7.38451442 8.20866984
7.75347613 6.05042283 -1.5177961 1.63986675 0.49238999
1.79996216 1.53487563 2.91938045 3.96941736 3.72906202
5.29228529 6.09923383 6.4043698 7.71071583 9.89709574
11.66055487 8.77146048 9.22566166 5.25029049 2.21001871
1.23637234 -1.53122158 -0.74989901 -1.78515003 -4.46331176
-2.33272877 7.82206596 5.39225348 0.4477594 -7.48053616
-7.35252969 -10.17397659 -10.84974438 -18.96382949 -14.47229699
-10.1171689 -6.7924112 -0.60745088 4.1423469 -4.08374483
1.66686436 -3.59396109 1.46103336 -0.36198973 -3.23440817
-6.78805453 -10.5830078 -8.82990086 -1.60890746 1.55953759
-2.40164873 -4.75697716 -3.66276138 -5.04571551 -8.3975777
-6.64870505 -9.32108339 -5.16698731 -2.21935132 -0.55302917
3.09405129 1.41543392 6.80927668 5.32080795 4.03642415
2.80136222 -0.48883997 0.98091035 -9.3109311 -10.44975233
-12.17866167 -7.76721224 -6.70244126 -5.71005459 -3.16672069
-1.60962546 1.22796987 3.33973187 4.10902026 2.4938628
2.09873924 2.23522455 6.7293423 10.2458385 11.98649859
14.51277627 15.33610972 12.3592922 3.30950649 -1.33009001
-7.70064119 -16.2598075 -21.93643588 -23.99441286 -21.57281831
-22.09948362 -19.01902913 -15.42032405 -10.21526342 -1.2848286
10.00583212 14.01444448 13.26503613 14.58564373 11.78781674
16.05519509 14.2503565 9.25884496 8.18146781 5.49270281
3.68162089 1.26707596 -5.1837924 -15.33943761 -20.94338746
-21.70813651 -24.10885703 -25.62638717 -22.01488214 -20.26368873
-6.81621086 -3.60503791 4.37861639 10.99665665 12.31394397
13.55862845 17.46635322 19.7972591 19.36270089 20.2461415
17.89914118 19.8141947 10.70295136 2.73354461 -3.90648664
3.20994417 -7.66620674 -6.03680965 -14.33137459 -14.55909668
-14.25459512 -13.6417409 -13.18028179 -9.88838174 -6.15664644
-2.57758209 -0.40965275 3.63030121 2.69225304 1.83118533
-0.76305452 -1.35694225 -2.31469117 -2.5698209 -2.02308717
-1.23587283 1.31682226 1.54072819 4.41996507 6.65604271
7.42649267 8.75310656 8.3500146 5.30094893 4.65446374
1.13634363 -5.87921235 -6.14424863 -7.1427953 -8.72636737
-7.38041198 -6.22284464 1.8054942 3.65688145 3.4468986
7.9682314 10.26900066 16.76646304 11.52810878 18.49644363
12.22306276 10.99972726 4.65025447 -3.49172699 -4.23351387
-9.04981844 -10.16925991 -12.31648932 -10.66801447 -8.02264203
-10.29512847 0.92347402 0.40377735 2.56023044 5.01908242
9.82158326 13.18762772 10.64186119 13.99175761 16.74536385
14.54825862 17.15089807 9.51623426 14.90346444 11.36194326
9.75801909 13.83487623 13.28143568 11.3004596 9.64609293
4.62038937 0.67058895 0.48645663 -0.69339491 -1.98314461
-3.057537 -3.0385244 -3.14042835 -3.3616465 -2.75316779
-4.56660318 -4.54727463 -4.37422336 -4.79124547 -4.6624152
-6.87485743 -10.72496848 -5.48967112 -4.13443411 -4.49878891
0.57070371 4.00859802 4.4958958 4.17028036 0.51264235
4.19680217 2.28483223 0.61515117 -2.8770441 -8.58384197
-12.58717262 -14.84903835 -15.36512005 -19.3821849 -16.86825967]
[[-7.19472573e-02 4.39589985e-04 -1.26497088e+01]
[-6.79137004e-02 6.39540190e-02 -1.24511874e+01]
[-5.28497903e-02 5.98267823e-02 -7.41837614e+00]
...
[-6.38121424e-03 -1.52709465e-03 -1.53651201e+01]
[-3.68542750e-02 9.68125944e-03 -1.93821849e+01]
[-6.52826291e-02 3.81614762e-02 -1.68682597e+01]]
(360, 3)
percentage for r: 68.61111111111109%
percentage for theta: 69.72222222222221%
percentage for f: 71.66666666666666%
Confidence intervals:
r: -0.012695034780607338 [-0.05974251647391811,0.09160519192667442]
theta: 0.0591173817297924 [-0.13850161343699083,0.038780451762357414]
f: 4.213571848652585 [-16.45978972464301,7.796742501146689]
Gaussian fit results:
r: 0.0016369867586912513 +-0.05666830422231802
theta: 0.0011412734863823432 +-0.06936185610143586
f: -0.44459354320907907 +-10.079416052542014
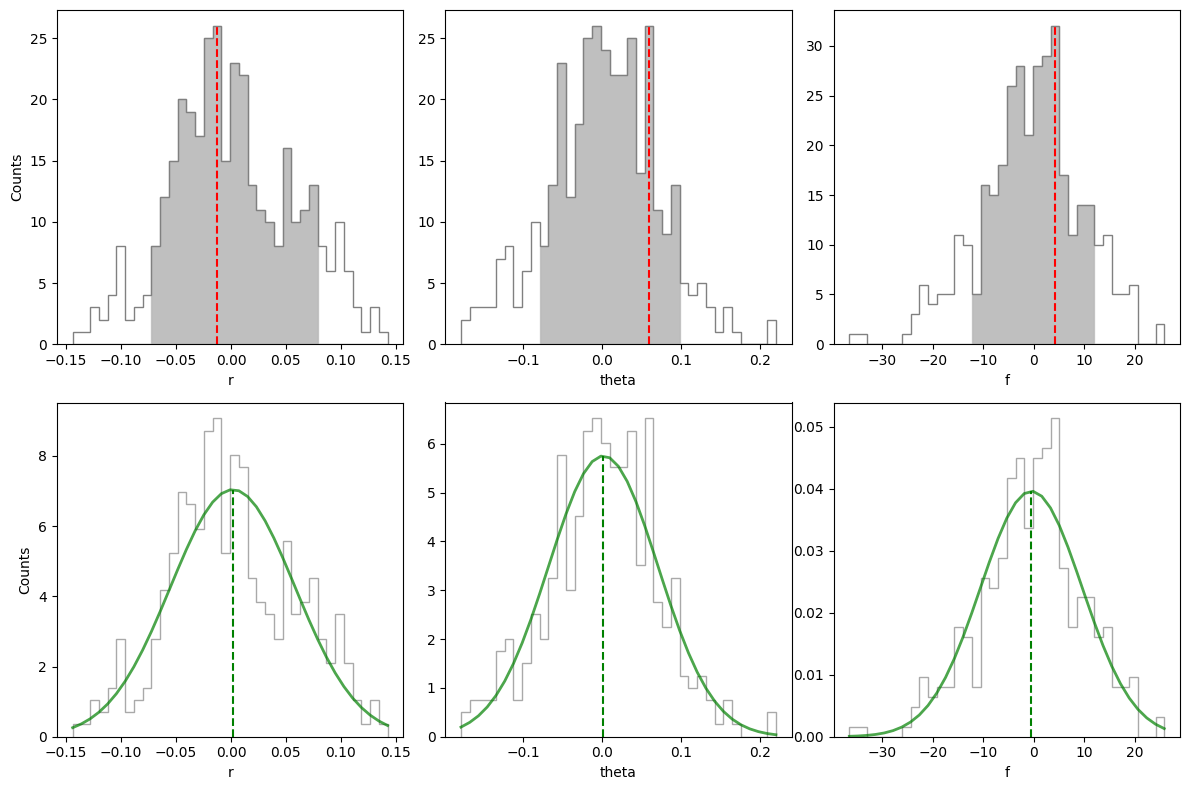
Again, if you wish to write the result (to avoid having to run the previous box again), just set write=True. This will pickle the result:
[50]:
write=False
if write:
output = {'speckle_res':speckle_res}
with open('../datasets/my_speckle_residuals_results', 'wb') as fileSave:
pickle.dump(output, fileSave)
Load pickled results from disk:
[51]:
with open('../datasets/speckle_residuals_results','rb') as fi:
myPickler = pickle.Unpickler(fi)
sp_unc_result = myPickler.load()
print(sp_unc_result.keys())
speckle_res = sp_unc_result['speckle_res']
sp_unc, mean_dev, p_simplex, offset, chi2, nit, success = speckle_res
dict_keys(['speckle_res'])
The speckle uncertainty associated to each parameter is contained in sp_unc which corresponds to the 1\(\sigma\) width of a Gaussian distribution fitted to the offset distribution (i.e. the differences with respect to injected ground truths):
[52]:
sp_unc
[52]:
array([ 0.05350939, 0.07376633, 10.64773837])
For comparison, the uncertainties found by the MCMC procedure (which also include Poisson noise) were:
[53]:
sigma
[53]:
array([ 0.13676103, 0.15744912, 21.66963444])
5.3.6. Final uncertainties
The final uncertainties on the planet parameters should include both statistical and systematic uncertainties. The former include both the photon noise and residual speckle noise uncertainties discussed above. The latter include both the uncertainty on the star location (which may be non-negligible when using a coronagraph) and instrumental calibration errors, including:
the uncertainty on the plate scale (for \(r\), when converting to angular separation) - note that it is proportional to the radial separation itself;
the uncertainty on the PA of true north (for \(\theta\)).
The uncertainty on the star location is of the order of 0.3px in individual NACO+AGPM images (this is the typical precision by manual recentering during the observation). Given the shift plots in Tutorial 2, it appears the autocorrelation timescale is of the order of ~5 frames. Therefore, considering that there are 61 frames in the datacube, the uncertainty on the star location in the final combined image must be roughly:
[54]:
cen_unc_indiv = 0.3 #px
cen_unc = cen_unc_indiv/np.sqrt(61/5) #px
cen_unc
[54]:
0.08588975014708022
The latter can be translated into an uncertainty on \(\theta\) by division by the radial separation of the companion. The stellar centering uncertainties on each planet parameter can thus be expressed as:
[55]:
star_unc = np.array([cen_unc*pxscale_naco,
np.rad2deg(cen_unc/val_max['r']),
0]) # uncertainty on each of the 3 parameters due to stellar centering
where the multiplication by pxscale_naco has converted the radial separation in arcsec.
For the instrumental calibration errors, we adopt the values quoted in Absil et al. (2013). Note that the uncertainty related to the plate scale is directly proportional to the radial separation of the companion.
[56]:
dr_unc = 0.00004 # plate scale uncertainty in arcsec per px
tn_unc = 0.09 # uncertainty on true north in deg
syst_unc = np.array([val_max['r']*dr_unc,
tn_unc,
0])
The final uncertainties are then the different sources of uncertainty added quadratically - after conversion of the radial separation to arcsec:
[57]:
sigma[0] *= pxscale_naco
sp_unc[0] *= pxscale_naco
if mu_sigma:
final_unc = np.sqrt(np.power(sigma,2) + np.power(star_unc,2) + np.power(syst_unc,2))
else:
final_unc = np.sqrt(np.power(sigma,2) + np.power(sp_unc,2) + np.power(star_unc,2) + np.power(syst_unc,2))
[58]:
msg = "The final estimates on the radial separation, PA and flux of the companion, including uncertainties, are: \n"
msg+= "r = {:.2f}+-{:.2f} mas (GT: {:.2f} mas), \n"
msg+= "PA = {:.2f}+-{:.2f} deg (GT: {:.2f} deg) \n"
msg+= "f = {:.2f}+-{:.2f} ADUs (GT: {:.2f} ADUs)"
print(msg.format(val_max['r']*pxscale_naco*1000, final_unc[0]*1000, rad_fc*pxscale_naco*1000,
val_max['theta'], final_unc[1], theta_fc,
val_max['f'], final_unc[2], flux_fc))
The final estimates on the radial separation, PA and flux of the companion, including uncertainties, are:
r = 831.33+-4.78 mas (GT: 829.29 mas),
PA = 239.92+-0.25 deg (GT: 240.00 deg)
f = 390.77+-24.14 ADUs (GT: 400.00 ADUs)
Let’s consider the Gaussian fit instead:
[59]:
msg = "Considering a Gaussian fit to the posterior distributions, the final estimates on the radial separation, PA and flux of the companion, including uncertainties, are: \n"
msg+= "r = {:.2f}+-{:.2f} mas (GT: {:.2f} mas), \n"
msg+= "PA = {:.2f}+-{:.2f} deg (GT: {:.2f} deg) \n"
msg+= "f = {:.2f}+-{:.2f} ADUs (GT: {:.2f} ADUs)"
print(msg.format(mu[0]*pxscale_naco*1000, final_unc[0]*1000, rad_fc*pxscale_naco*1000,
mu[1], final_unc[1], theta_fc,
mu[2], final_unc[2], flux_fc))
Considering a Gaussian fit to the posterior distributions, the final estimates on the radial separation, PA and flux of the companion, including uncertainties, are:
r = 830.00+-4.78 mas (GT: 829.29 mas),
PA = 239.95+-0.25 deg (GT: 240.00 deg)
f = 394.13+-24.14 ADUs (GT: 400.00 ADUs)
[ ]: